2.2.3. Détermination de la taille minimum de
l'échantillon
Comme vu dans le paragraphe
précédent,20 410 clients constituent la population cible. A
défaut de temps et des moyens, nous ne pouvonsmener l'étude sur
tous les clients. Ainsi,Nous avons effectué un
échantillonaléatoire simple; et pour déterminer notre
échantillon, nous nous sommes servi de la formule tirée du cours
de technique d'enquête qui donne "n" la taille de
l'échantillon: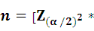 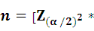 S2x] /e2 S2x] /e2
Où :
· n : est taille de
l'échantillon,
· Zá /2: valeur
tirée de la loi normale au seuil á(fixée
à 1.96)
· á : L'intervalle de confiance
ou seuil de risque (fixé à 5%)
· Sx: Ecart type de
l'échantillon ;
· e : 0,05 C'est la marge d'erreur
choisi par le chercheur.
A partir de la formule, on remarque que la taille
cherchée est fonction de l'écart-type de l'échantillon qui
n'est pas connu à priori. Ainsi, l'inconnu n'étant fonction d'une
autre inconnue l'écart-type, il en découle un paradoxe. La
théorie propose trois solutions pour résoudre le problème
:
- Avoir des informations empiriques sur le problème
étudié,
- Procéder à une pré-enquête
permettant de déterminer l'écart type.
- Ou utiliser les cas des proportions avec p égale 0,5
dans la mesure où cette valeur donne p(1-p) égale à 0,25
qui est la variance la plus élevée permettant des tailles
élevées.
Etant donné l'absence des informations
antérieures sur la satisfaction des clients des institutions
financières de la ville Goma, nous avons opté pour une
pré-enquête.
Notre pré-enquête a porté sur 30 clients
proportionnellement extraits des 3IMF. Le traitement des données
relatives à ces 30 clients dégage une satisfaction moyenne de 3,7
avec un écart-type de 0,505. Ayant toutes les données
nécessaires (écart-type = 0,505 et marge de précision
acceptée = 5%), nous avons déterminé la taille de
l'échantillon grâce à la formule susmentionnée.
Ainsi donc : n = [(1.96)2 * (0.505)2] /
(0.05)2
= (3.8416 * 0.25) / 0.0025
= 0.9604 / 0.0025
= 384.16
= 384clients
Nous aurons donc à mener une étude de
comparaison de satisfaction sur 384 clients répartis de manière
stratifiée les IMF. La table ci-dessous synthétise les
informations sur la réparation de l'échantillon pour
l'enquête.
| 


