2.3.Comparaison des performances entre les modèles
VECM et BSVAR
Dans ce cadre, pour procéder à une comparaison
des performances entre le modèle VECM et le modèle BSVAR, nous
comparons les deux modèles en s'appuyant sur le critère de
l'erreur quadratique moyenne de prévision. Ensuite, nous utiliserons le
test de Diebold- Mariano pour analyser la significativité de
différence des deux modèles en termes d'erreur de
prévision. Enfin, nous terminerons notre travail de comparaison par le
test de Harvey, Leybourne et Newbold pour voir s'il y a un modèle qui
pourrait expliquer la prévision combinée.
2.3.1. Critère de l'Erreur Quadratique Moyenne de
Prévision
Considérons deux modèles
économétriques ??1 et ??2 qui expliquent les variables ???? pour
?? ? (1, ??). Découpons l'intervalle en deux tel que : (1, ??) = (1,
??0) ? (??0, ??), nous estimons les deux modèles
considérés sur la période (1, ??0), et sur la
base des résultats, nous formons deux séries de
prévisions, ??????,1 et
??????,2sur l'intervalle (??0, ??). L'EQMP est
calculée en se basant sur les observations réelles sur
l'intervalle (??0, ??). Par conséquent, nous obtiendrons :
?????????? = v?? ((??*??,?? - ??*)2)
???????? ??* = (????0, ... , ????) ???? ??*??,?? =
(????0??,??, ??????,??).
62
Nous rappelons que notre base de données contient 64
observations, s'étalant du T1 2006 jusqu'au T4 2021. Ainsi, pour
effectuer notre démarche de comparaison, nous passons principalement par
les étapes suivantes :
- Nous estimons les deux modèles pour une série
d'observations allant du T1 2006 au T2 2019, et nous simulerons les
prévisions sur les 10 périodes restantes.
- Ensuite, pour la deuxième étape, nous
considérons pour les estimations la période du T1 2006 au T1
2018, et nous simulerons les prévisions pour les 15 périodes
restantes. - Enfin, les prévisions simulées s'étaleront
sur 20 périodes entre T1 2017 et le T4 2021. Sur la base des
différentes prévisions simulées, nous calculerons l'EQMP
variable par variable et du modèle, une valeur plus petite indique une
meilleure performance du modèle.
Tableau 10 : Les résultats de l'indice EQMP
|
EQMP
|
Différence VECM
BSVAR
|
|
VECM
|
B-SVAR
|
|
NPL
|
7.665
|
3.932
|
3.733
|
|
ROA
|
0.940
|
0.814
|
0.126
|
|
PCC
|
1.416
|
0.284
|
1.132
|
|
10 périodes
|
IPC
|
0.008
|
0.025
|
-0.017
|
|
IPI
|
0.070
|
0.129
|
-0.060
|
|
TMM
|
1.399
|
1.702
|
-0.303
|
|
USD
|
0.313
|
0.450
|
-0.137
|
|
TOTAL
|
11.810
|
7.336
|
7.475
|
|
NPL
|
14.218
|
5.798
|
8.419
|
|
ROA
|
0.761
|
1.600
|
-0.839
|
|
PCC
|
2.466
|
0.264
|
2.202
|
|
15 périodes
|
IPC
|
0.013
|
0.094
|
-0.081
|
|
IPI
|
0.063
|
0.127
|
-0.064
|
|
TMM
|
0.875
|
1.146
|
-0.271
|
|
USD
|
0.252
|
0.247
|
0.005
|
|
TOTAL
|
18.648
|
9.278
|
9.370
|
|
NPL
|
14.210
|
2.265
|
11.945
|
|
ROA
|
6.124
|
5.470
|
0.654
|
|
PCC
|
2.418
|
0.971
|
1.447
|
|
20 périodes
|
IPC
|
0.062
|
0.097
|
-0.035
|
|
IPI
|
0.057
|
0.122
|
-0.065
|
|
TMM
|
2.435
|
2.392
|
0.043
|
|
USD
|
0.259
|
0.492
|
-0.233
|
|
TOTAL
|
25.566
|
11.811
|
13.755
|
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
D'après le tableau ci-dessus, nous remarquons que d'un
point de vue global, le modèle BSVAR offre dans tous les cas des
meilleures prévisions que celles produites par le modèle VECM, vu
que l'indice de l'EQMP du modèle BSVAR est plus faible que celui du
modèle VECM. Par conséquent, l'intégration de l'approche
bayésienne a amélioré la précision du
modèle.
63
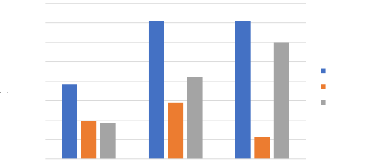
Ainsi, le graphique ci-dessous nous montre la
différence entre les erreurs de prévision des NPL des deux
modèles. Nous observons une différence croissante entre les
erreurs des deux modèles, passant de 3,7% sur 10 périodes
à 11,9% sur 20 périodes. Cela prouve clairement que le
modèle BSVAR possède une meilleure robustesse et stabilité
au fil du temps. (Annexe12)
Figure 4 : EQMP des NPL
10 Période 15 Période 20
Période
16.0%
14.0%
12.0%
10.0%
NPL
8.0%
6.0%
4.0%
2.0%
0.0%
14.2% 14.2%
7.7%
3.9%3.7%
5.8%
8.4%
11.9%
2.3%
VECM BSVAR Différences
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
Nous pouvons conclure que l'introduction de l'identification
structurel et l'information à priori ont améliorer le potentiel
de précision de la modélisation. En effet, la
considération d'une information supplémentaire a un effet positif
sur les prévisions des NPL. Cependant, il faut vérifier que cette
différence est significative statistiquement. Pour résoudre ce
problème, nous recourons au test de Diebold-Mariano.
| 


