III. L'APPLICATION DU MODELE A LA BASE DE DONNEES
Dans cette section, nous nous proposons d'étudier le
contrôle des biais; nous montrons comment nous avons tenté de
contrôler les principaux biais suivants : le biais stratégique, le
biais de point de départ et le biais hypothétique.
Nous calculerons ensuite les déterminants de la
disposition des individus à contribuer à l'éducation de
leurs enfants. L'on suppose que cette variable pourrait être
expliquée par les variables que nous avons présentées au
point un.
22
III-1- Contrôle des biais
III-1-1 Contrôle du biais stratégique
Le biais stratégique survient lorsque les personnes
interrogées donnent à dessein des réponses fausses,
sachant que dans la réalité elles ne devront effectuer aucun
paiement. Ce biais survient également lorsque les individus pensent que
leurs réponses auront une influence sur la décision finale,
à savoir : Réduire les coûts liés à
l'éducation. Ils proposent donc souvent des sommes dérisoires,
voire nulles. Ce biais implique que les individus ont une bonne connaissance
des conséquences de leurs réponses. Ce biais a été
corrigé en intégrant les questions suivantes dans le
questionnaire, pour des individus proposant des sommes nulles :
C-16/ Are you ready to pay something for the
education of your child?
Yes (Go to C-18) NO (Go to C -17)
C- 17/ Do you thing that the responsibility
for the education of your children in the primary falls entirely on the
state?
Yes NO
III-1-2 Contrôle du biais de point de
départ : Test des moyennes de Student
Pour tester l'existence de ce biais, nous avons posé
la même question aux enquêtés sous des formes
différentes : Sous la forme de la méthode des enchères et
celle de la carte de paiement.
Les tableaux ci-dessous exposent les résultats du test
du biais du point de départ. Il montre que la deuxième question
donne un consentement moyen à cotiser inférieur à celui
obtenu avec la première question.
Nous utiliserons le test de Student de comparaison de deux
moyennes. III-1-2-1 Définition et présentation du test
Un test d'hypothèse est une démarche qui a pour
but de fournir une règle de décision permettant, sur la base des
résultats d'échantillon, de faire un choix entre deux
hypothèses statistiques :
? L'hypothèse nulle H0 qui est l'hypothèse que
l'on souhaite invalider ; en effet, il est plus facile de rejeter une
hypothèse (un seul contre-exemple suffit), alors que valider une
hypothèse demande de rechercher toutes les situations possibles et de
vérifier qu'aucune d'entre-elle ne contredise cette hypothèse.
? L'hypothèse alternative H1 est l'hypothèse
qui sera retenue au cas où le test statistique rejette
l'hypothèse nulle H0.
La conclusion qui sera déduite des résultats de
l'analyse aura un caractère probabiliste : On ne pourra prendre une
décision qu'en ayant conscience qu'il y a un certain risque qu'elle soit
erronée. Ce risque nous est donné par le seuil de signification
du test (á)
Pour ce test, H0 est l'hypothèse selon laquelle les
deux moyennes sont identiques, et H1 l'hypothèse selon laquelle les 2
moyennes sont différentes.
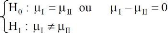
23
Dans le cadre de notre étude, nous effectuerons des
tests au seuil de 10%, 5 % et 1 %. La table des valeurs usuelles pour une
distribution de Student nous donne les valeurs respectives de 1, 6; 1,96 et
2,58.
| 


