II.1.b. Introduction historique des Équations
Dans la classe choisie pour cette expérience par Madame
LAZARO, le QCM a été fait en amont du nouveau chapitre. Il s'est
avéré que les élèves avaient peu de souvenirs de
5ème, seulement 60% d'entre eux savaient résoudre une
équation (présentée comme une opération à
trou), 30% ont su vérifier une égalité, et enfin 40%
traduire un problème simple en équation. Ces premiers
résultats ont donc été un peu moins bons que dans la
classe de Mme FRACKOWIAK dans l'ensemble.
La première activité introduisant la
séquence « équations » s'est faite autour de l'Histoire
de cette notion. En effet, nous sommes « partis » le temps d'une
séance en 300 avant JC, au temps du mathématicien Euclide, en
Grèce antique. Pour commencer la séance et capter l'attention des
élèves, leur professeur a lu une petite introduction
résumant la biographie d'Euclide et la principale de ses oeuvres :
Éléments. Les élèves ont
écouté avec attention et dans un silence inhabituel. Ensuite, les
sujets d'activité ont été distribués (annexe
3) et la classe a pu découvrir la présence de sept phrases
bien mises en évidence comme si elles avaient été
écrites à la plume. Madame LAZARO a alors formé des
groupes de trois élèves, mélangeant leurs niveaux et leur
implication habituelle dans le cours. Chaque trio devait analyser une des sept
phrases, qui étaient en réalité des postulats
écrits par Euclide dans les Éléments, en faisant
une lecture synchronique au sens de Fried : traduction dans notre
système de notation actuel des Mathématiques anciennes.
Le travail s'est poursuivi dans le calme, chaque membre de
chaque groupe exprimant son idée, comme si leur
hétérogénéité s'était effacée.
Les élèves ont écrit une trace de leurs idées sur
une feuille et ont dû passer au tableau devant leurs camarades groupe
après groupe pour présenter le postulat qu'ils avaient à
étudier. Comme attendu, les résultats présentés par
les élèves n'ont pas été très bons, ils ont
eu du mal à transcrire en langage mathématique actuel les phrases
en langage naturel d'Euclide. Le but de cette activité n'était
pas qu'ils réussissent cette retranscription, mais qu'ils essaient. En
essayant, ils se sont rendus compte du grand écart de notation entre
l'antiquité et nos jours. Leur captivation pour cette
étrangeté, de ne pas réussir complètement à
traduire une phrase en apparence simple, a servi de tremplin à Madame
LAZARO pour présenter la notion d'équation et ses
propriétés contenues dans les postulats. Une mise en commun a
donc été faite, jusqu'à aboutir avec
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
20
l'enseignante aux phrases et propriétés
mathématiques attendues. Une fois que les élèves ont
compris le principe avec les premiers postulats, leur professeur leur a
donné un peu de temps supplémentaire pour réussir seuls
à (re)transcrire les autres, ce qui a été plus facile
cette fois.
Ainsi, les élèves ont écrit par
eux-mêmes, bien qu'ils aient été débloqués
par leur professeur, leurs premières équations en
découvrant les propriétés. Madame LAZARO a profité
de cette activité pour montrer aux élèves à quel
point les notations mathématiques avaient évolué avec le
temps, entre la phrase naturelle d'Euclide et l'ensemble des symboles, chiffres
et lettres d'aujourd'hui. Cela a permis aux élèves de constater
la vertu épistémologique de l'Histoire comme
l'énonçait Barbin. En effet ils ont pu se rendre compte de
l'évolution du concept étudié. L'illustration suivante a
été projetée au tableau :
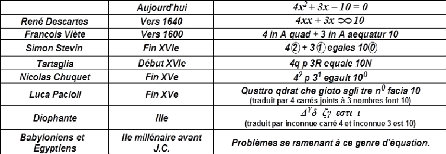
Présentation d'une équation à
travers les époques
La suite de la séquence s'est poursuivie de
manière plus classique, mais chaque résolution d'équation
a remémoré aux élèves leur activité au temps
d'Euclide, ils arrivaient donc à utiliser les propriétés
correctement, sans trouver cela trop abstrait comme dans la classe avec la
présentation classique. Les résultats des évaluations de
fin de chapitre ont d'ailleurs été significatifs : nous pouvons
constater que 80% des élèves de la classe ont réussi
à traduire un énoncé. De même, 80% ont su
résoudre une équation. Les élèves semblent donc
avoir acquis, pour ce devoir, les compétences visées et cela de
manière plus significative que dans la classe de Madame FRACKOWIAK. Pour
la dernière compétence, 70% des élèves ont su
tester une égalité. L'avancée ici est à peu
près similaire à l'autre classe.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
21
On peut donc penser que l'Histoire des Mathématiques a
eu un impact sur les résultats des élèves. Les
élèves ont pu se rattacher à l'activité
d'introduction durant toute la séquence pour progresser dans la
méthode de résolution d'équations. Nous espérons
donc avoir réussi à leur faire comprendre le sens des
équations à travers l'étude de leur Histoire.
| 


