Memoire Online - L'histoire des mathématiques et la motivation des élèves.

De nombreux chercheurs ont tenté de catégoriser les recherches sur l'introduction de l'Histoire des Mathématiques dans l'enseignement.

C'est le cas de d'Uffe Thomas Jankvist, un enseignant-chercheur de l'Université Aarhus au Danemark. En 2009, dans son article A categorization of the « whys » and « hows » of using History in Mathematics education^*, il mène un travail important sur une distinction entre deux aspects de l'utilisation de l'Histoire dans l'enseignement et l'apprentissage des Mathématiques et leurs corrélations. Nous allons étudier ses recherches ici.

* Catégorisation des « pourquoi » et « comment » dans l'utilisation de l'Histoire dans l'enseignement des Mathématiques

LAZARO Virginie Mémoire 'Histoire des Mathématiques et motivation des élèves'

Tout d'abord, Jankvist parle des méthodes utilisées pour introduire l'Histoire des Mathématiques en classe : le « comment ». Il y a selon lui trois façons d'introduire et de présenter la dimension historique dans l'enseignement des Mathématiques.

Premièrement, il y a l'approche anecdotique : il s'agit d'introduire en début ou en fin de cours, ou de séquence, des faits isolés, des capsules historiques ou anecdotes particulières. Ce sont des interventions brèves, isolées, où le professeur fait part de quelques informations historiques : noms de Mathématiciens, dates, et problèmes qu'ils ont étudiés par exemple. Cette méthode est très utilisée au Québec, où notamment Lindstrom (1995) a créé dans son manuel des petites rubriques historiques à chaque fin de chapitre concernant les notions abordées.

Ensuite, Jankvist parle de l'approche par module d'apprentissage. Cette méthode plus répandue consiste en des capsules d'Histoire plus importantes. Elles peuvent être sous la forme d'activités autour de l'Histoire, ou de parties de séquences d'enseignement qui peuvent occuper plusieurs cours entiers. Il peut s'agir de lectures de textes historiques, d'études de situations-problèmes ou de projets de recherche menés par les élèves. Les textes étudiés sont eux-mêmes classés en deux catégories : les sources primaires et les sources secondaires. Un texte de catégorie dite « primaire » est un texte original écrit par un Mathématicien. À sa lecture, un élève ou un étudiant peut s'en faire sa propre interprétation et ses propres conclusions. D'un autre côté, un texte de catégorie « secondaire » est déjà passé entre les mains d'historiens ou d'experts en Mathématiques. Ici, les traductions puis améliorations en langage moderne peuvent biaiser les idées que voulait faire passer l'auteur. En lisant ce type de document, les élèves perçoivent l'interprétation de celui qui a manipulé le texte et qui l'a retranscrit. C'est une approche différente.

Enfin, la troisième méthode citée par Jankvist est l'approche historique intégrée. Cette approche diffère des précédentes car elle consiste en un mode d'élaboration inscrit dans le temps. Lorsqu'un enseignant utilise ce mode de présentation, il suit en réalité l'ordre chronologique, donc historique, d'apparition des notions. Par exemple, lors de l'introduction des types de nombres, le professeur parle d'abord des entiers naturels, puis des rationnels positifs, ensuite de quelques irrationnels (toujours positifs) avant de retourner « avant » le zéro et donc de considérer les nombres négatifs, puis les réels et enfin les complexes. Cet ordre est exactement celui dans lequel les types de nombres ont été « trouvés », du moins

LAZARO Virginie Mémoire 'Histoire des Mathématiques et motivation des élèves'

considérés, car pendant longtemps les hommes ne voulaient pas concevoir la notion de nombres négatifs. De cette façon, les élèves ont parfois accès à des branches des Mathématiques hors-programme mais nécessaires à l'avancée chronologique vers l'objectif du programme.

Dans un second temps, Jankvist parle des arguments appuyant l'introduction historique des Mathématiques : le « pourquoi ». Il y a deux visions différentes de cette utilité.

Pour commencer, l'Histoire des Mathématiques peut être vue comme un outil motivationnel pour les élèves lorsqu'elle est introduite en classe. Elle accompagne l'enseignement des Mathématiques et permet une humanisation de la discipline. Aussi, cet outil peut aider à montrer que les Mathématiques « ne tombent pas du ciel ». Les notions du programme prennent une nouvelle dimension moins abstraite, les élèves découvrent leurs origines et quelques détails de leurs évolutions au cours du temps. L'introduction de l'Histoire des Mathématiques peut donc susciter l'intérêt des élèves pour cette discipline. Jankvist précise que l'approche historique est considérée comme un outil si l'intention du professeur reste sur l'objet mathématique à enseigner.

D'autre part, Jankvist parle de l'Histoire des Mathématiques comme un objectif en soi. Cette fois l'intention du professeur est portée sur l'Histoire elle-même, et l'apprentissage de « l'esprit mathématique ». Dans cette optique, on considère tout le raisonnement philosophique et socio-culturel qui a animé les mathématiciens de tous temps dans leurs recherches. On voit non seulement la finalité du cours qui est l'apprentissage d'une notion du programme, mais aussi tout le contexte de la pensée et les barrières rencontrées aux différentes étapes d'élaboration des notions, comme si les élèves devenaient des Thalès, Euclide ou Fermat. Ils constatent donc d'eux-mêmes que les Mathématiques sont en constante évolution dans le temps et dans l'espace, et que cette évolution est semée d'embûches et d'impasses.

Dans son article, Jankvist parle de la nécessité de faire la distinction entre le « pourquoi » et le « comment », ce qui est peu fait dans la littérature. Il faut éviter toute confusion entre méthode et argument. Distinguer les deux aspects ne veut pas dire les isoler, Jankvist aborde d'ailleurs les interrelations entre ces deux aspects de recherche. Pour mieux

LAZARO Virginie Mémoire 'Histoire des Mathématiques et motivation des élèves'

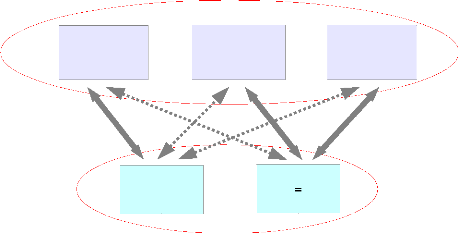
comprendre cela, prenons un exemple : imaginons que l'on veuille faire une approche anecdotique d'une notion, il semble inadapté de considérer alors l'Histoire comme un objectif en soi. Elle est donc vue comme un outil. En revanche, l'approche historique intégrée peut la considérer comme un objectif en soi. Ces interrelations peuvent être illustrées par le schéma suivant, qui récapitule aussi toute la catégorisation.

Légende :

: interrelations plus adaptées

: interrelations moins adaptées

Ainsi, cette étude sur la catégorisation des « pourquoi » et « comment » de l'utilisation de l'Histoire dans l'enseignement des Mathématiques de Jankvist nous permet d'éclaircir les méthodes et aspects de l'enseignement de notre discipline aux élèves. Cela s'avérera très utile lors de notre expérimentation pour ne pas se perdre dans trop de manières différentes d'introduire l'Histoire des Maths dans nos classes, et nous permettra de distinguer clairement nos objectifs.

L'histoire des mathématiques et la motivation des élèves.

I.2. Le « Pourquoi » et le « Comment » selon Jankvist