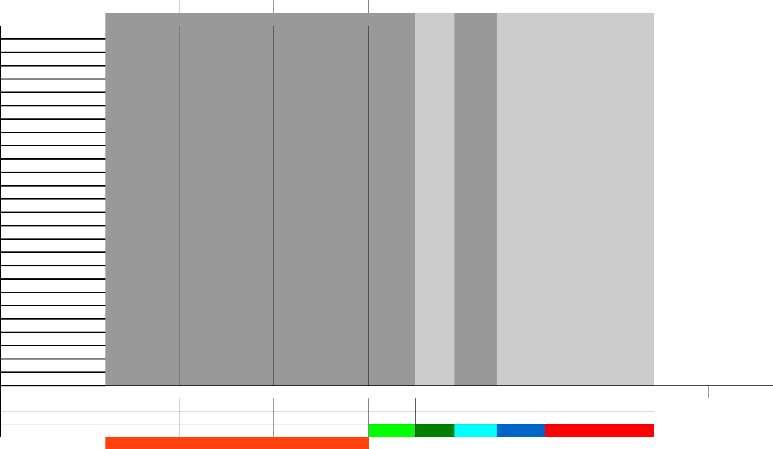
Annexe 1. QCM Equations
67
Moyenne opérations
après
avant
après après
Addition à trou
Soustraction à trou
Multiplication à trou
Tester une égalité Traduire un énoncé
Résoudre une équation
Nombre bonnes réponses
avant avant avant avant
|
Élève 1
|
oui oui oui oui oui oui oui oui non non oui oui non oui oui non
non oui non oui oui oui oui non non non oui
|
oui oui oui oui oui oui oui oui oui oui oui non non oui oui non
oui oui non non oui oui non non oui oui oui
|
oui non oui oui oui oui non non non non oui oui non oui oui non
oui oui non non non oui oui non non oui non
|
oui oui
non non
oui oui
oui oui
non oui
non oui
non non
oui non
non oui
non non
oui oui
non oui
oui oui
oui non
non oui
non oui
non non
non non
non non
non oui
non oui
non non
non oui
oui oui
oui oui
oui oui
non oui
|
non oui
oui non
oui non
oui oui
non oui
oui oui
non non
non non
non non
non non
non oui
oui oui
oui oui
oui oui
non oui
non non
oui oui
non oui
oui non
non oui
non non
non non
oui oui
oui oui
oui non
non oui
non oui
|
oui oui oui oui oui oui oui non oui oui oui oui oui oui oui non
non oui oui oui oui non oui oui non oui oui
|
|
Élève 2
|
|
Élève 3
|
|
Élève 4
|
|
Élève 5
|
|
Élève 6
|
|
Élève 7
|
|
Élève 8
|
|
Élève 9
|
|
Élève 10
|
|
Élève 11
|
|
Élève 12
|
|
Élève 13
|
|
Élève 14
|
|
Élève 15
|
|
Élève 16
|
|
Élève 17
|
|
Élève 18
|
|
Élève 19
|
|
Élève 20
|
|
Élève 21
|
|
Élève 22
|
|
Élève 23
|
|
Élève 24
|
|
Élève 25
|
|
Élève 26
|
|
Élève 27
|
|
Pourcentage réussite
|
|
nombre de oui
|
18
|
20
|
14
|
10
|
18
|
12
|
16
|
22
|
|
nombre de non
|
9
|
7
|
13
|
17
|
9
|
15
|
11
|
5
|
|
% réussite
|
69
|
77
|
54
|
38
|
69
|
46
|
62
|
85
|
|
Avant
|
Après
|
|
4
|
3
|
|
3
|
1
|
|
5
|
2
|
|
5
|
3
|
|
3
|
3
|
|
4
|
3
|
|
2
|
1
|
|
3
|
0
|
|
1
|
2
|
|
1
|
1
|
|
4
|
3
|
|
3
|
3
|
|
2
|
3
|
|
5
|
2
|
|
3
|
3
|
|
0
|
1
|
|
3
|
1
|
|
3
|
2
|
|
1
|
1
|
|
1
|
3
|
|
2
|
2
|
|
3
|
0
|
|
3
|
3
|
|
2
|
3
|
|
3
|
1
|
|
3
|
3
|
|
2
|
3
|
|
55
|
69
|
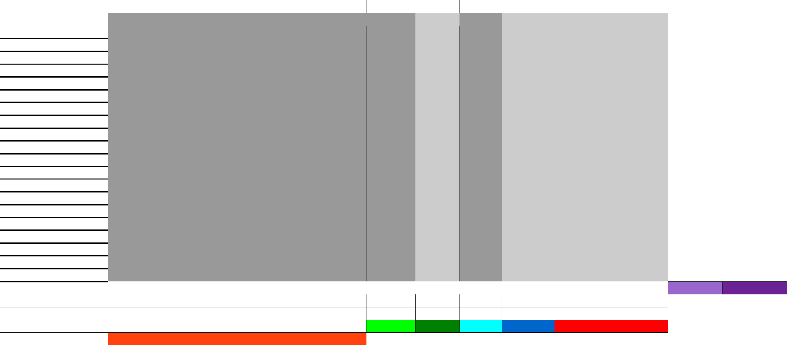
avant
après
après après
Moyenne opérations
60
Addition à trou
Soustraction à trou
Multiplication à trou
Tester une égalité
Traduire un énoncé Résoudre une
équation
Nombre bonnes réponses
avant avant avant avant
|
Élève 1
|
oui oui oui oui oui non oui oui oui oui non non oui oui oui oui
oui non oui non
|
non non oui oui oui non oui non oui oui non oui oui non oui oui
oui non non non
|
non non oui non oui non oui non oui oui non non oui oui oui non
oui oui non non
|
non non
non non
non oui
oui oui
non oui
non non
oui oui
non oui
oui oui
oui oui
non oui
non oui
non oui
non oui
oui oui
non oui
oui non
non non
non oui
non non
|
non non
non oui
non oui
oui oui
oui oui
non non
oui oui
non oui
oui oui
oui oui
oui oui
non non
oui oui
non oui
non oui
oui oui
non oui
non oui
non non
non oui
|
non oui oui oui oui non oui oui oui oui non oui oui oui oui oui
oui oui non oui
|
|
Élève 2
|
|
Élève 3
|
|
Élève 4
|
|
Élève 5
|
|
Élève 6
|
|
Élève 7
|
|
Élève 8
|
|
Élève 9
|
|
Élève 10
|
|
Élève 11
|
|
Élève 12
|
|
Élève 13
|
|
Élève 14
|
|
Élève 15
|
|
Élève 16
|
|
Élève 17
|
|
Élève 18
|
|
Élève 19
|
|
Élève 20
|
|
Pourcentage réussite
|
|
nombre de oui
|
15
|
11
|
10
|
6
|
14
|
8
|
16
|
16
|
|
nombre de non
|
5
|
9
|
10
|
14
|
6
|
12
|
4
|
4
|
|
% réussite
|
75
|
55
|
50
|
30
|
70
|
40
|
80
|
80
|
|
Avant
|
Après
|
|
1
|
0
|
|
1
|
2
|
|
3
|
3
|
|
4
|
3
|
|
4
|
3
|
|
0
|
0
|
|
5
|
3
|
|
1
|
3
|
|
5
|
3
|
|
5
|
3
|
|
1
|
2
|
|
1
|
2
|
|
4
|
3
|
|
2
|
3
|
|
4
|
3
|
|
3
|
3
|
|
4
|
2
|
|
1
|
2
|
|
1
|
1
|
|
0
|
2
|
|
50
|
77
|
4ème A la découverte des
équations en Grèce antique
Euclide est un Mathématicien de la Grèce
antique ayant vécu environ en 300 avant J-C. Vous en avez
déjà entendu parler notamment en étudiant la «
division euclidienne ».
Son ouvrage le plus célèbre s'appelle Les
« Éléments », dans lequel il parle de
géométrie et d'arithmétique théorique. On trouve
dans ce livre des théorèmes et leurs démonstrations, mais
aussi des postulats et des axiomes : ce sont des propriétés, des
vérités qui sont admises et que l'on ne démontre pas. Nous
allons en étudier quelques uns, en essayant de les traduire en
Mathématiques modernes.
Par groupes de trois élèves désignés
par le professeur :
a. Expliquer avec vos mots sur une feuille
(avec vos noms) ce que vous comprenez du postulat d'Euclide qui correspond au
numéro de votre groupe.
b. Essayer de traduire ce postulat avec des
symboles mathématiques (+, -, =, x, a,...)
Voici la liste des postulats d'Euclide:
1. Les choses égales à une même
chose sont égales entre elles.
2. Si à des choses égales, on ajoute
des choses égales, les touts seront
.égaux.
3. Si à des choses égales, on retranche
des choses égales, les restes seront
égaux.
4. Si à des choses inégales, on ajoute
des choses égales, les touts seront
inégaux.
5. Si à des choses inégales, on
retranche des choses égales, les restes seront
inégaux.
6. Les choses, qui sont doubles d'une même
chose, sont égales entre elles.
7. Les choses, qui sont les moitiés d'une
même chose, Sont égales entre elles.
c. Groupe par groupe, passer au tableau pour
expliquer à vos camarades ce que vous avez trouvé.
4ème Activité : A la découverte du
Théorème de Thalès en Égypte
« Appuyé sur la rambarde d'un bateau,
Thalès regardait s'éloigner la terre de Milet où il avait
vécu jusqu'à ce jour. Il partait pour l'Égypte.
Après quelques jours de voyage, non loin de la rive du fleuve, il
l'aperçut. La pyramide de Khéops. Thalès
n'avait jamais rien vu d'aussi grand. Un matelot dit à Thalès :
"Cette pyramide a été dressée par le pharaon Khéops
dans le seul but d'obliger les humains à se persuader de leur petitesse.
Le but est atteint. Pharaon et ses architectes ont voulu nous contraindre
à admettre qu'entre cette pyramide et nous il n'y a aucune
commune mesure". C'était une évidence pour tout le monde
: la hauteur de la pyramide était impossible à mesurer. Elle
était la construction la plus visible du mondé habité et
elle était la seule à ne pouvoir être mesurée !
Thalès voulut relever ce défi.
Un matin, lorsque le soleil éclaira l'horizon, debout,
Thalès regarda se déployer son ombre sur le sable. Plus le soleil
montait dans le ciel, plus son ombre devenait petite, jusqu'à faire la
même taille que lui à 10 heures... »

Étape 1. L'Égypte miniature au lever du
Soleil
Nous plongeons la classe dans l'obscurité. Nous avons face
à nous, en miniature :
- Un bâton représentant Thalès (Hauteur : 2
cm)
- Une pyramide en papier (Hauteur : Inconnue)
- Une lampe pour la lumière du Soleil.
Quelques uns d'entre vous vont pouvoir tenir la lampe et ainsi
produire un lever de Soleil sur notre
petit montage. Observez bien tous la situation.
a. De retour à votre place, imaginez comment, grâce
à ce matériel, mesurer la hauteur réelle de la pyramide en
papier. (Rappelez-vous qu'elle représente une immense pyramide
impossible à mesurer directement). Écrivez le protocole (la
méthode) à suivre sur la feuille blanche distribuée.
b. Par groupes de 4 élèves désignés
par le professeur, discutez de vos méthodes pour mesurer la hauteur de
la pyramide en papier. Comparez et sélectionnez la méthode qui
vous semble la meilleure. Écrire cette méthode (si elle est
différente de la votre) sur votre feuille.
c. Un représentant de chaque groupe est choisi. Il vient
sur le montage et explique devant tous ses camarades la méthode
adoptée par son groupe (il peut être aidé d'un ou plusieurs
camarades si besoin). Il l'exécute et dit à tout le monde la
hauteur qu'il a trouvé pour la pyramide en papier. Notez ici les
résultats des différents groupes :
Groupe A : cm Groupe C : cm Groupe E : cm
Groupe B : cm Groupe D : cm
d. La vraie hauteur de la pyramide en papier est (attendre que
le professeur vous
donne cette mesure). Discussions autour des
résultats obtenus. Puis, le professeur explique comment Thalès a
réellement pu mesurer la hauteur de la pyramide de Khéops
(animation).
4C Effectuer une Recherche : Pour le
22/01/2015
-Expliquez qui était Thalès.
-Expliquez avec vos propres mots comment Thalès a
mesuré la pyramide de Khéops. Vous pouvez effectuer un dessin
pour compléter votre texte.

Diapo 2 Diapo 6
Diapo 3 Diapo 7
Diapo 4 Diapo 8
Diaporama réalisé par les 3 élèves
de Madame Frackowiak
Diapo 1 Diapo 5
Questionnaire : Motivation
Consigne : Lis chaque affirmation
attentivement. Réponds le plus honnêtement possible en entourant
à chaque fois le numéro qui correspond le mieux à ce que
tu penses.
1
Tout à fait faux
2
Plutôt faux
3
Un peu faux
4
Un peu vrai
5
Plutôt vrai
6
Tout à fait vrai
J'aime les Mathématiques.
1
|
2
|
3
|
4
|
5
|
6
|
2- L'Histoire des Mathématiques me permet d'apprendre
beaucoup de choses utiles.
|
1
|
2
|
3
|
4
|
5
|
6
|
3- Je fais des Mathématiques pour obtenir une belle
récompense.
|
1
|
2
|
3
|
4
|
5
|
6
|
4- L'Histoire des Mathématiques m'intéresse
beaucoup.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|
5-J'ai choisi de faire de l'Histoire des Mathématiques
pour apprendre plein de choses.
|
1
|
2
|
3
|
4
|
5
|
6
|
|
6-Je fais de l'Histoire des Mathématiques pour faire
plaisir à mon enseignante.
|
1
|
2
|
3
|
4
|
5
|
6
|
7- Je fais des Mathématiques pour faire plaisirs à
mes parents et à mon enseignante.
|
1
|
2
|
3
|
4
|
5
|
6
|
8- J'étudie l'Histoire des Mathématiques
même lorsque je ne suis pas obligé de le faire.
|
1
|
2
|
3
|
4
|
5
|
6
|
9- Dans la vie il est important d'apprendre à faire des
Mathématiques.
|
1
|
2
|
3
|
4
|
5
|
6
|
10- Je fais des Mathématiques pour montrer aux autres
que je suis bon.
|
1
|
2
|
3
|
4
|
5
|
6
|
|
11- J'arrive toujours à finir les exercices sur le
|
1
|
2
|
3
|
4
|
5
|
6
|
|
théorème de Thalès.
|
|
|
|
|
|
|
|
12-J'arrive à me concentrer sur mes exercices sur le
|
1
|
2
|
3
|
4
|
5
|
6
|
|
théorème de Thalès en classe.
|
|
|
|
|
|
|
|
13-Je comprends les exercices qui utilisent le
théorème
|
1
|
2
|
3
|
4
|
5
|
6
|
|
de Thalès.
|
|
|
|
|
|
|
|
14-J'arrive à me motiver pour faire mes exercices sur
|
1
|
2
|
3
|
4
|
5
|
6
|
|
le théorème de Thalès.
|
|
|
|
|
|
|
|
15-Je suis capable de m'organiser pour faire mes
|
1
|
2
|
3
|
4
|
5
|
6
|
|
exercices sur le théorème de Thalès en
classe.
|
|
|
|
|
|
|
Feuille1
|
J'aime les mathématiques
|
L'histoire des mathématiques va me permettre d'apprendre
beaucoup de choses utiles.
|
Je fais des mathématiques pour obtenir une belle
récompense.
|
L'histoire des mathématiques m'intéresse
beaucoup.
|
J'ai choisi de faire de l'histoire des mathématiques pour
apprendre plein de choses.
|
Je fais de l'histoire des mathématiques pour faire plaisir
à mon enseignante.
|
Je fais des mathématiques pour faire plaisirs à mes
parents et à mon enseignante.
|
J'étudie l'histoire des mathématiques même
lorsque je ne suis pas obligé de le faire.
|
Dans la vie il est important d'apprendre à faire des
mathématiques.
|
Je fais des mathématiques pour montrer aux autres que je
suis bon.
|
Type de motivation de l'élève:
Intrinsèque, Extrinsèque ou Amotivation
Ext
Ext
Ext
A
Ext
Int-Ext Int
Int-Ext Int Ext Ext
Int-Ext Ext
Int-Ext Ext Ext Int Int Int
Élève 1
|
3
|
3
|
5
|
3
|
3
|
2
|
2
|
1
|
6
|
1
|
|
Élève 2
|
6
|
2
|
6
|
1
|
4
|
6
|
3
|
1
|
6
|
6
|
|
Élève 3
|
2
|
2
|
1
|
1
|
1
|
6
|
5
|
1
|
4
|
1
|
|
Élève 4
|
1
|
3
|
2
|
3
|
1
|
1
|
1
|
2
|
6
|
1
|
|
Élève 5
|
4
|
3
|
4
|
2
|
2
|
1
|
4
|
2
|
3
|
2
|
|
Élève 6
|
5
|
4
|
5
|
4
|
3
|
3
|
4
|
1
|
5
|
3
|
|
Élève 7
|
2
|
3
|
1
|
3
|
4
|
2
|
4
|
2
|
4
|
1
|
|
Élève 8
|
6
|
5
|
5
|
6
|
3
|
6
|
3
|
1
|
4
|
1
|
|
Élève 9
|
5
|
4
|
2
|
5
|
4
|
4
|
3
|
3
|
6
|
4
|
|
Élève 10
|
1
|
3
|
1
|
4
|
2
|
1
|
6
|
1
|
6
|
1
|
|
Élève 11
|
1
|
2
|
1
|
3
|
1
|
5
|
5
|
1
|
4
|
1
|
|
Élève 12
|
6
|
5
|
6
|
6
|
5
|
3
|
4
|
4
|
6
|
3
|
|
Élève 13
|
3
|
1
|
6
|
3
|
1
|
1
|
3
|
1
|
6
|
2
|
|
Élève 14
|
6
|
5
|
6
|
5
|
5
|
2
|
1
|
2
|
6
|
1
|
|
Élève 15
|
3
|
2
|
4
|
3
|
3
|
4
|
4
|
3
|
5
|
4
|
|
Élève 16
|
6
|
1
|
3
|
1
|
1
|
1
|
6
|
1
|
6
|
1
|
|
Élève 17
|
2
|
6
|
1
|
3
|
5
|
1
|
1
|
3
|
6
|
1
|
|
Élève 18
|
6
|
5
|
1
|
4
|
4
|
1
|
1
|
1
|
6
|
5
|
|
Élève 19
|
3
|
4
|
2
|
4
|
5
|
1
|
4
|
4
|
6
|
1
|
Page 1
Moy 3,7 3,3 3,3 3,4 3,0 2,7 3,4 1,8 5,3 2,1
|
motivation intrinsèque
|
Pourcentage motivation intrinsèque:
Pourcentage motivation extrinsèque: ge motivation
intrinsèque et extrinsèque: Pourcentage d'amotivation
:
|
26,3%
|
|
|
|
|
motivation extrinsèque
|
47,4 %
21,1 %
5%
|
Page 3
Feuille1
|
J'arrive toujours à finir les exercices sur le
théorème de Thalès.
|
J'arrive à me concentrer sur mes exercices sur le
théorème de Thalès en classe.
|
Je comprends les exercices qui utilisent le
théorème de Thalès.
|
J'arrive à me motiver pour faire mes exercices sur le
théorème de Thalès.
|
Je suis capable de m'organiser pour faire mes exercices sur le
théorème de Thalès en classe.
|
Moyenne élève Thalès
|
|
4
|
4
|
4
|
3
|
5
|
4,0
|
|
6
|
6
|
6
|
5
|
6
|
5,8
|
|
4
|
3
|
4
|
2
|
1
|
2,8
|
|
1
|
4
|
1
|
2
|
1
|
1,8
|
|
2
|
3
|
2
|
2
|
3
|
2,4
|
|
5
|
4
|
4
|
4
|
4
|
4,2
|
|
3
|
3
|
3
|
4
|
3
|
3,2
|
|
5
|
5
|
6
|
3
|
4
|
4,6
|
|
4
|
4
|
5
|
4
|
5
|
4,4
|
|
6
|
1
|
6
|
1
|
6
|
4,0
|
|
2
|
2
|
1
|
4
|
3
|
2,4
|
|
5
|
5
|
6
|
6
|
5
|
5,4
|
|
3
|
6
|
3
|
6
|
3
|
4,2
|
|
6
|
5
|
6
|
6
|
5
|
5,6
|
|
2
|
2
|
3
|
3
|
3
|
2,6
|
|
3
|
5
|
3
|
1
|
1
|
2,6
|
|
6
|
6
|
6
|
5
|
4
|
5,4
|
|
4
|
1
|
6
|
6
|
6
|
4,6
|
|
5
|
4
|
5
|
4
|
5
|
4,6
|
|
4,0
|
3,8
|
4,2
|
3,7
|
3,8
|
|
|
Moyenne Thalès:
|
3,9/6
|
Feuille1
|
Élève 1
|
4
|
4
|
1
|
3
|
1
|
1
|
2
|
1
|
4
|
4
|
|
Élève 2
|
1
|
5
|
2
|
3
|
1
|
1
|
1
|
1
|
6
|
2
|
|
Élève 3
|
1
|
2
|
1
|
1
|
1
|
6
|
6
|
1
|
6
|
2
|
|
Élève 4
|
6
|
3
|
2
|
4
|
2
|
3
|
4
|
1
|
5
|
5
|
|
Élève 5
|
1
|
3
|
1
|
4
|
1
|
1
|
1
|
1
|
5
|
1
|
|
Élève 6
|
5
|
3
|
1
|
3
|
2
|
1
|
2
|
4
|
6
|
2
|
|
Élève 7
|
3
|
5
|
2
|
1
|
2
|
6
|
6
|
1
|
4
|
3
|
|
Élève 8
|
4
|
4
|
2
|
2
|
2
|
5
|
5
|
2
|
4
|
1
|
|
Élève 9
|
4
|
4
|
3
|
2
|
3
|
1
|
1
|
3
|
6
|
4
|
|
Élève 10
|
5
|
4
|
1
|
6
|
4
|
1
|
1
|
4
|
5
|
4
|
|
Élève 11
|
2
|
3
|
1
|
1
|
1
|
4
|
4
|
1
|
2
|
1
|
|
Élève 12
|
4
|
2
|
1
|
3
|
3
|
4
|
3
|
2
|
4
|
4
|
|
Élève 13
|
6
|
6
|
6
|
1
|
6
|
1
|
1
|
1
|
6
|
1
|
|
Élève 14
|
5
|
6
|
2
|
5
|
6
|
1
|
1
|
4
|
6
|
1
|
|
Élève 15
|
6
|
4
|
2
|
4
|
4
|
2
|
1
|
1
|
5
|
1
|
|
Élève 16
|
5
|
3
|
1
|
4
|
1
|
2
|
3
|
2
|
5
|
3
|
|
Élève 17
|
3
|
2
|
5
|
2
|
2
|
2
|
4
|
2
|
6
|
1
|
|
Élève 18
|
5
|
2
|
3
|
2
|
3
|
1
|
1
|
1
|
3
|
3
|
|
Élève 19
|
6
|
4
|
2
|
4
|
4
|
4
|
4
|
4
|
5
|
1
|
Type de motivation de l'élève:
Intrinsèque, Extrinsèque ou Amotivation
|
J'aime les mathématiques
|
L'histoire des mathématiques va me permettre d'apprendre
beaucoup de choses utiles.
|
Je fais des mathématiques pour obtenir une belle
récompense.
|
L'histoire des mathématiques m'intéresse
beaucoup.
|
J'ai choisi de faire de l'histoire des mathématiques pour
apprendre plein de choses.
|
Je fais de l'histoire des mathématiques pour faire plaisir
à mon enseignante.
|
Je fais des mathématiques pour faire plaisirs à mes
parents et à mon enseignante.
|
J'étudie l'histoire des mathématiques même
lorsque je ne suis pas obligé de le faire.
|
Dans la vie il est important d'apprendre à faire des
mathématiques.
|
Je fais des mathématiques pour montrer aux autres que je
suis bon.
|
Int Int Ext Int-Ext
A
Int Ext Ext Int Int Ext
Int-Ext
Int-Ext Int Int Int Ext
A
Int-Ext
Page 1
Moy 4,0 3,6 2,1 2,9 2,6 2,5 2,7 1,9 4,9 2,3
|
motivation intrinsèque
|
Pourcentage motivation intrinsèque:
Pourcentage motivation extrinsèque: ge motivation
intrinsèque et extrinsèque: Pourcentage d'amotivation
:
|
42,1%
|
|
|
|
|
motivation extrinsèque
|
26,3%
21,1 %
11%
|
Page 3
Feuille1
|
J'arrive toujours à finir les exercices sur le
théorème de Thalès.
|
J'arrive à me concentrer sur mes exercices sur le
théorème de Thalès en classe.
|
Je comprends les exercices qui utilisent le
théorème de Thalès.
|
J'arrive à me motiver pour faire mes exercices sur le
théorème de Thalès.
|
Je suis capable de m'organiser pour faire mes exercices sur le
théorème de Thalès en classe.
|
Moyenne élève Thalès
|
|
4
|
3
|
3
|
2
|
2
|
2,8
|
|
3
|
3
|
4
|
4
|
3
|
3,4
|
|
4
|
3
|
3
|
1
|
1
|
2,4
|
|
5
|
6
|
6
|
6
|
4
|
5,4
|
|
3
|
2
|
2
|
1
|
6
|
2,8
|
|
1
|
1
|
1
|
1
|
1
|
1,0
|
|
6
|
6
|
4
|
4
|
6
|
5,2
|
|
4
|
2
|
2
|
2
|
1
|
2,2
|
|
4
|
4
|
4
|
2
|
3
|
3,4
|
|
4
|
2
|
2
|
1
|
1
|
2,0
|
|
5
|
4
|
4
|
2
|
3
|
3,6
|
|
5
|
4
|
5
|
4
|
4
|
4,4
|
|
6
|
6
|
6
|
6
|
6
|
6,0
|
|
5
|
6
|
6
|
6
|
6
|
5,8
|
|
5
|
5
|
5
|
5
|
5
|
5,0
|
|
5
|
4
|
5
|
3
|
5
|
4,4
|
|
5
|
6
|
6
|
5
|
6
|
5,6
|
|
5
|
5
|
6
|
4
|
3
|
4,6
|
|
5
|
5
|
5
|
5
|
5
|
5,0
|
|
4,4
|
4,1
|
4,2
|
3,4
|
3,7
|
|
|
Moyenne Thalès:
|
3,9/6
|
Feuille1
|
Élève 1
|
5
|
4
|
4
|
3
|
4
|
4
|
2
|
2
|
4
|
3
|
|
Élève 2
|
5
|
6
|
1
|
6
|
6
|
1
|
1
|
3
|
6
|
1
|
|
Élève 3
|
4
|
3
|
3
|
4
|
5
|
1
|
1
|
1
|
6
|
3
|
|
Élève 4
|
5
|
2
|
3
|
1
|
4
|
2
|
2
|
1
|
5
|
2
|
|
Élève 5
|
4
|
1
|
5
|
1
|
1
|
3
|
4
|
1
|
6
|
1
|
|
Élève 6
|
5
|
4
|
4
|
3
|
3
|
6
|
4
|
1
|
4
|
1
|
|
Élève 7
|
1
|
1
|
1
|
2
|
1
|
1
|
3
|
1
|
6
|
3
|
|
Élève 8
|
4
|
5
|
4
|
2
|
4
|
1
|
5
|
1
|
6
|
1
|
|
Élève 9
|
4
|
6
|
5
|
4
|
5
|
4
|
3
|
4
|
6
|
4
|
|
Élève 10
|
5
|
2
|
3
|
4
|
4
|
1
|
1
|
2
|
6
|
1
|
|
Élève 11
|
1
|
2
|
6
|
1
|
1
|
1
|
6
|
1
|
2
|
1
|
|
Élève 12
|
4
|
2
|
4
|
2
|
2
|
2
|
2
|
2
|
6
|
2
|
|
Élève 13
|
3
|
3
|
1
|
2
|
4
|
2
|
1
|
1
|
5
|
1
|
|
Élève 14
|
5
|
2
|
2
|
1
|
4
|
1
|
1
|
4
|
6
|
4
|
|
Élève 15
|
1
|
1
|
2
|
1
|
4
|
1
|
5
|
1
|
2
|
1
|
|
Élève 16
|
2
|
4
|
4
|
2
|
3
|
1
|
5
|
6
|
5
|
1
|
|
Élève 17
|
3
|
4
|
6
|
3
|
3
|
3
|
4
|
2
|
5
|
3
|
|
Élève 18
|
3
|
1
|
1
|
3
|
2
|
2
|
2
|
1
|
5
|
2
|
|
Élève 19
|
4
|
5
|
5
|
3
|
2
|
1
|
1
|
2
|
6
|
1
|
|
Élève 20
|
2
|
1
|
3
|
2
|
3
|
2
|
2
|
1
|
4
|
2
|
|
Élève 21
|
6
|
5
|
5
|
4
|
4
|
2
|
1
|
4
|
5
|
2
|
|
Élève 22
|
5
|
1
|
3
|
1
|
1
|
1
|
1
|
1
|
6
|
1
|
|
Élève 23
|
5
|
4
|
4
|
3
|
3
|
3
|
4
|
2
|
6
|
5
|
|
Élève 24
|
3
|
4
|
2
|
2
|
3
|
4
|
1
|
4
|
5
|
2
|
|
Élève 25
|
3
|
1
|
4
|
3
|
4
|
3
|
6
|
1
|
6
|
6
|
|
Élève 26
|
5
|
3
|
1
|
4
|
3
|
4
|
2
|
2
|
1
|
1
|
Type de motivation de l'élève:
Intrinsèque, Extrinsèque ou Amotivation
|
J'aime les mathématiques
|
L'histoire des mathématiques va me permettre d'apprendre
beaucoup de choses utiles.
|
Je fais des mathématiques pour obtenir une belle
récompense.
|
L'histoire des mathématiques m'intéresse
beaucoup.
|
J'ai choisi de faire de l'histoire des mathématiques pour
apprendre plein de choses.
|
Je fais de l'histoire des mathématiques pour faire plaisir
à mon enseignante.
|
Je fais des mathématiques pour faire plaisirs à mes
parents et à mon enseignante.
|
J'étudie l'histoire des mathématiques même
lorsque je ne suis pas obligé de le faire.
|
Dans la vie il est important d'apprendre à faire des
mathématiques.
|
Je fais des mathématiques pour montrer aux autres que je
suis bon.
|
Int-Ext*
Int
Int
Int
Int-Ext*
Int-Ext
A
Int-Ext
Int-Ext
Int
Ext
Int-Ext
Int*
Int
Ext
Int-Ext
Int-Ext
Int
Int-Ext
A
Int-Ext
Int Int-Ext Int-Ext
Ext
Int-Ext
Moy 3,7 3,0 3,3 2,6 3,2 2,2 2,7 2,0 5,0 2,1
motivation intrinsèque motivation extrinsèque
élève orateur
30,4%
13,0%
47,8 %
9 % * : ne compte pas
Page 1
Pourcentage motivation intrinsèque: Pourcentage
motivation extrinsèque: ge motivation intrinsèque et
extrinsèque:
Pourcentage d'amotivation :
Feuille1
J'arrive toujours à finir les exercices sur le
théorème de Thalès.
J'arrive à me concentrer sur mes exercices sur le
théorème de Thalès en classe.
Je comprends les exercices qui utilisent le
théorème de Thalès.
J'arrive à me motiver pour faire mes exercices sur le
théorème de Thalès.
Je suis capable de m'organiser pour faire mes exercices sur le
théorème de Thalès en classe.
Moyenne élèves exposés
Thalès
Moyenne autres élèves
Thalès
Page 3
3
|
4
|
4
|
4
|
4
|
3,8
|
|
|
3
|
6
|
4
|
5
|
6
|
|
4,8
|
|
5
|
5
|
4
|
5
|
4
|
|
4,6
|
|
5
|
5
|
6
|
3
|
5
|
|
4,8
|
|
5
|
6
|
6
|
4
|
4
|
5
|
|
|
4
|
4
|
4
|
3
|
4
|
|
3,8
|
|
1
|
5
|
5
|
4
|
5
|
|
4,0
|
|
4
|
1
|
2
|
3
|
3
|
|
2,6
|
|
3
|
5
|
4
|
4
|
3
|
|
3,8
|
|
6
|
5
|
6
|
4
|
6
|
|
5,4
|
|
1
|
1
|
1
|
1
|
1
|
|
1,0
|
|
5
|
5
|
6
|
4
|
6
|
|
5,2
|
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
6
|
5
|
6
|
1
|
6
|
|
4,8
|
|
6
|
4
|
5
|
5
|
4
|
|
4,8
|
|
5
|
4
|
5
|
4
|
5
|
|
4,6
|
|
2
|
3
|
4
|
4
|
4
|
|
3,4
|
|
4
|
4
|
5
|
4
|
3
|
|
4,0
|
|
3
|
2
|
3
|
5
|
5
|
|
3,6
|
|
1
|
1
|
1
|
2
|
2
|
|
1,4
|
|
5
|
6
|
5
|
6
|
6
|
|
5,6
|
|
5
|
5
|
6
|
3
|
5
|
|
4,8
|
|
3
|
5
|
4
|
3
|
3
|
|
3,6
|
|
3
|
5
|
4
|
3
|
4
|
|
3,8
|
|
2
|
4
|
4
|
5
|
5
|
|
4,0
|
|
5
|
6
|
5
|
4
|
6
|
|
5,2
|
|
3,7
|
4,1
|
4,2
|
3,6
|
4,2
|
|
|
|
Moyenne Thalès:
|
4,1/6
|
|
|


