II.3.b. Analyse des recherches individuelles
La réalisation de ces recherches individuelles peut
être vue comme une approche anecdotique au moment de la mise en commun
des recherches mais c'est surtout une approche par module selon Jankvist au
niveau du travail individuel de chaque élève. Peu d'entre eux ont
cité leurs sources, on ne peut donc pas dire si les documents qu'ils ont
étudiés pour leur recherche étaient de catégorie
primaire ou secondaire. Cependant, nous imaginons qu'ils se sont dirigés
vers des sites Internet où les informations ont déjà
été traitées pour faciliter la
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
29
compréhension du lecteur. Quoiqu'il en soit, l'Histoire
des Mathématiques est restée un outil. Ici elle sert
nécessairement à faire passer une notion essentielle du programme
: le théorème de Thalès. Nous pensons avoir en partie
franchi les obstacles rencontrés habituellement durant cette
séquence par l'utilisation de l'Histoire des Mathématiques. En
effet l'étude de l'expérience de Thalès a permis de mettre
en avant la nécessité de l'hypothèse des droites
parallèles. De plus, Thalès a utilisé un bâton dont
il connaissait la mesure, a attendu d'obtenir une ombre égale à
la longueur de ce bâton au sol pour en déduire la taille de
l'ombre de la pyramide et donc sa hauteur. C'est un raisonnement de
proportionnalité que les élèves ont tous compris en
recherchant.
Le fait d'avoir acquis des connaissances historiques sur le
théorème a d'une part permis de surmonter certains obstacles
didactiques, mais elle a également eu des effets sur la motivation. Les
premiers signes visibles ont été ceux observés en classe.
Les élèves se sont beaucoup impliqués lors de la mise en
commun des recherches. Tous ont participé, même les plus
réservés. Chacun cherchait à aller plus loin dans la
précision des réponses apportées par ses camarades. Les
seconds effets visibles ont été ceux observés dans les
copies rendues par les élèves (une copie est proposée en
annexe 9). Ainsi on a pu voir des schémas précis, ou des
dessins illustratifs. Certains textes sur la mesure de la pyramide ont
été romancés. Ainsi on a pu observer que les
élèves ont voulu transmettre le fruit de leurs recherches avec
beaucoup d'application et d'envie.
Enfin le dernier instrument de mesure de la motivation
était celui du questionnaire (annexe 8b). Les premières
questions ont permis de mettre en évidence que :
· 42,1% des élèves de la première
classe de Madame FRACKOWIAK furent motivés intrinsèquement
· 26,3% furent motivés extrinsèquement
· 21,1% furent motivés à la fois
intrinsèquement et extrinsèquement
· 11% furent amotivés
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
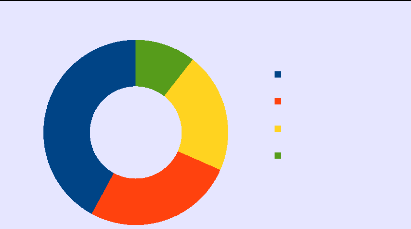
Motivation et recherches individuelles
Pourcentage motivation intrinsèque:
Pourcentage motivation extrinsèque:
Pourcentage motivation intrinsèque et
extrinsèque:
Pourcentage d'amotivation :
30
Ici, on constate que pour cette approche par module de
l'Histoire, les élèves de Madame FRACKOWIAK semblent
majoritairement avoir été motivés intrinsèquement.
Ce qui correspond à un plaisir réel d'accomplir la tâche
demandée.
La deuxième partie du questionnaire a permis de
déterminer l'intensité de cette motivation décelée
chez la plupart des élèves. La moyenne des points de SEP
évaluée dans cette classe est également de 3,9 points sur
6. Ce qui est tout aussi satisfaisant que dans l'expérience
précédente.
Nous pensons que l'élément motivationnel majeur
de cette expérimentation, qui explique les résultats
observés, est la nouveauté liée à l'introduction de
l'Histoire des Mathématiques. Il s'agit d'une motivation
intrinsèque. Nous pouvons tenter d'expliquer ce succès par
plusieurs facteurs :
Ø Nouveauté de la situation d'apprentissage
(motivation extrinsèque)
Ø L'élève se sent responsable dans
l'acquisition des savoirs (motivation intrinsèque)
Ø Réponse aux exigences de l'enseignant
(motivation extrinsèque)
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
31
| 


