II.2.3. Clipping
251654144Dans cette partie, on ne s'intéresse qu'au
problème du clipping d'un segment par un rectangle.
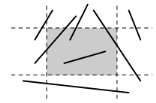
Figure II.4: Ensemble de droites. La zone de
clipping est déterminée par les droites en
pointillés.
Pour le résoudre, on utilise l'algorithme de
Cohen-Sutherland. Et l'algorithme renvoie la partie du segment incluse dans le
rectangle et rien si le segment n'en fait pas partie. Et voici son
algorithme :
Segment COHEN-SUTHERLAND ( rectangle [Pmin,Pmax], segment
[P1,P2])
1. déterminer les codes binaires B1 et B2 de P1 et P2
2. si B1 =0et B2 =0alors retourner P1, P2. sinon si B1&B2
=0 alors retourner rien. sinon
(a) si B1 =0alors P1 =INTERSECTION([Pmin,Pmax],[P1,P2], B1)
(b) si B2=0alors P2 =INTERSECTION([Pmin,Pmax],[P2,P1], B2)
(c) retourner COHENSUTHERLAND([Pmin,Pmax],[P1, P2])
et la fonction Intersection par :
point INTERSECTION(rectangle [Pmin,Pmax], segment [Pd,Pf],
byte B,)
1. si le 1er bit de B =1 alors P =intersection du segment
[Pd,Pf] avec x = xmin.
2. si le 2`eme bit de B =1 alors P =intersection du segment
[Pd,Pf] avec x = xmax.
3. si 3`eme bit de B =1 alors P =intersection du segment
[Pd,Pf] avec y = ymin.
4. si 4`eme bit de B =1 alors P =intersection du segment
[Pd,Pf] avec y = ymax.
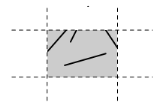
5. retourner P.
Figure II.5: Résultat
Note : L'Algorithme de Cohen-Sutherland
peut se généraliser en 3D en utilisant des plans à la
place de droite. Une de ses utilisations pratiques est de simplifier
(après rejet trivial) la géométrie à
l'extérieur du cône de vision pour ne conserver dans la
chaîne de traitement que les polygones observables ou partiellement
observables. La définition des plans associés au cône de
vision sera détaillée dans le point suivant.
| 


