II.6. Réponse d'un
système
II.6.1. Réponse d'un
système du premier ordre
1. Mise en équation
 (2.4) (2.4)
T,K : sont des réels positifs
 (2.5) (2.5)
La fonction de transfert s'écrit
 (2.6) (2.6)
K : gain statique, T : constante de temps. (temps
requis pour que le signal de sortie atteigne 63% du signal d'entrée
lorsque cette dernière est un échelon et ce pour un
système du première ordre)
2. Réponses
2.1. Réponse impulsionnelle
(E(p)=1)
 (2.7) (2.7)
En appliquant Laplace inverse, on passe du domaine de Laplace
ou domaine temporel.
 (2.8) (2.8)
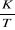
s(t)
t
Figure 2.7. Réponse impulsionnelle d'un
système du premier ordre
2.2. Réponse indicielle ( ) )
 (2.9) (2.9)
En utilisant les tables des transformées de Laplace
 (2.10) (2.10)
s(t) K
0,63K
t
T 3T
Figure 2.8. Réponse indicielle d'un système
du premier ordre
T est le temps nécessaire pour atteindre 63% de sa
valeur à l'infinie
3T est le temps nécessaire pour atteindre 95 % de sa
valeur à l'infinie
Le temps de réponse Tr = 3T, est le temps au
bout duquel la sortie atteint sa valeur asymptotique (sa valeur à
l'infinie) à 5 % près.
Preuve
 (2.11) (2.11)


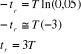
 (2.12) (2.12)
2.3. Réponse à une entrée
rampe ( ) )
 (2.13) (2.13)
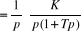
Il est clair que cette sortie et la primitive de la
sortie :
 (2.13) (2.13)
En appliquant Laplace
 (2.14) (2.14)
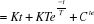
à t=0
s(0)=KT+Cte=0
Cte=-KT
 (2.15) (2.15)
S(t) e(t)=t (entrée)
Asymptote y=K(t-T)
t
Figure 2.9. Réponse d'un système du premier
ordre à entrée rampe
II.6.1. Réponse d'un
système du second ordre
1. Mise en équation
Les systèmes du second ordre sont régis par des
équations différentielles du second degré, leur fonction
de transfert comporte un maximum de deux zéros et deux pôles.
L'équation courante est du type :
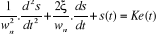 (2.16) (2.16)
Les 3 constantes  : pulsation propre : pulsation propre
 : coefficient ou facteur d'amortissement : coefficient ou facteur d'amortissement
K, gain statique du système
(sont réels et généralement
positifs).
En appliquant Laplace (voir annexe)
 (2.17) (2.17)
La fonction de transfert
 (2.18) (2.18)
 (2.19) (2.19)
2. Réponses
2.1. Réponse indicielle ( ) )
 (2.20) (2.20)
La factorisation du dénominateur est dotée par
le discriminant (delta) du trinôme.
 (2.21) (2.21)
Et
 (2.22) (2.22)
La littérature offre trois cas. 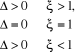
1er cas : 
 (2.23) (2.23)
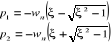 (2.24) (2.24)
S(t)
K 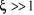
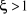
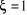
t
t
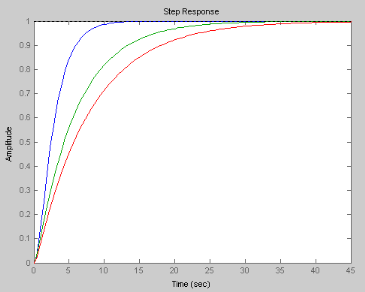
Figure 2.10. Réponse indicielle d'un système du
second ordre ( ) )
La réponse la plus rapide est observée pour  très proche de 1 très proche de 1
2ème cas : 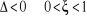
Le trinôme possède alors deux racines complexes
conjuguées qui sont :
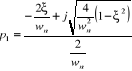 (2.25) (2.25)
 (2.26) (2.26)
 (2.27) (2.27)
S(t) est la réponse du système, constituée
de la différence de deux signaux :
· Le signal k.u(t), échelon de hauteur K
· Le signal sinusoïdal encadré par une enveloppe
e, exponentielle décroissant tendant vers zéro en oscillant.
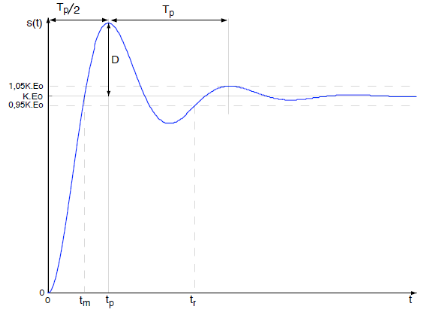
Figure 2.11. Réponse indicielle d'un système du
second ordre à coefficient d'amortissement inférieur à 1
( ) )
La réponse du système est bien dépendant
de 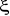
 : Régime amorti : Régime amorti
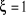 : Régime critique sans oscillation : Régime critique sans oscillation
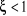 : Régime oscillatoire amorti, : Régime oscillatoire amorti,
| 


