II.3. Fonction de transfert
d'un système linéaire
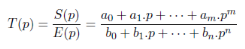
On appelle fonction de transfert ou transmittance d'un
système linéaire le rapport entre la transformée de
Laplace de la sortie sur celle de l'entrée :
(2.1)
C'est une fonction rationnelle. L'ordre du système (qui
est l'ordre de l'équation différentielle) est le degré du
dénominateur de T(p).
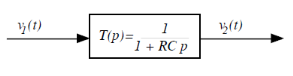
Figure 2.4. Schéma fonctionnel d'un Circuit
RC
On identifiera facilement le fait que c'est un système
d'ordre 1 dont la constante de temps est = RC et de gain statique K = 1.
II.4. Réponse
temporelle des systèmes
On veut caractériser les systèmes d'une part par
leur fonction de transfert et, d'autre part, par leur comportement. Ce dernier
peut être mis en évidence par la réponse s(t) à une
entrée donnée. Classiquement, on peut apprendre beaucoup des
systèmes en observant la réponse aux entrées suivantes
:
- l'impulsion : réponse impulsionnelle
- l'échelon : réponse indicielle
- la rampe : la réponse à une entrée
rampe
- la sinusoïde : réponse
fréquentielle
Nous étudierons aux points suivants les réponses
des systèmes et allons faire le lien entre fonction de transfert et les
réponses (c'est à dire les réponses aux impulsions,
échelon et rampe). Comme dans la suite, nous allons étudier les
systèmes simples et très répandus que sont les
systèmes du premier ordre et du second ordre. De plus, les
méthodes d'étude de ces systèmes se
généralisent facilement aux autres.
II.5. Les
différentes entrées classiques
II.5.1. L'échelon
C'est l'entrée la plus utilisée de toutes. Elle
correspond à un changement brusque de consigne. Cette fonction est
définie par :
  , a R*
et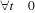  
Sa transformée de Laplace est :
 (2.2)
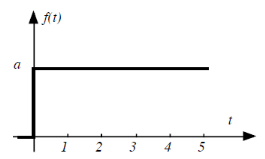
Figure 2.5. La fonction échelon
On appelle échelon unitaire la fonction dont la TL est
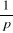 (a = 1). On le note souvent u(t). On appelle réponse indicielle
la réponse à l'échelon unité. (Cfr. Annexe).
II.5.2. La rampe
La rampe de pente a est la primitive de l'échelon de
hauteur a. Elle est définie par :
 
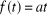
et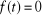  
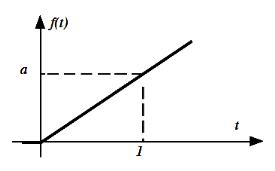
Figue 2.6. La fonction rampe de pente a
Sa transformée de Laplace est définie par :
 (2.3)
On peut définir également la rampe unitaire : la
rampe de pente 1.
II.5.3. L'impulsion
L'impulsion unité est, dans l'espace des distributions,
la dérivée de l'échelon unitaire. On l'appelle aussi
impulsion de Dirac.
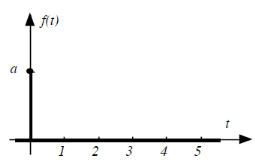
Figure2.7. La fonction impulsion de Dirac de poids
a
| 
