Analyse du comportement de la servovalve electro-hydraulique lors de freinage des roues d'un avion (cas de Boeing 737-NG)

II.2. Equations d'un système linéaire

Dans toute la suite du cours, les systèmes considères n'auront qu'une entrée et qu'une sortie.

II.2.1. Introduction

Un système est dit linéaire si l'équation liant la sortie à l'entrée est une équation différentielle linéaire à coefficients constants. La forme générale de cette équation différentielle est :

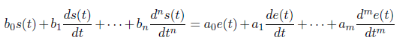
III.2.2. Exemples

R

Soit le circuit RC

C

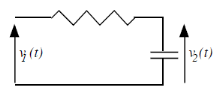
Figure 2.3. Circuit RC

v₁ =e(t) et v₂=s(t)

Les équations électriques sont :

e(t) = R.i + s(t)

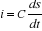
, introduisant Laplace dans les deux membres, il vient :

, et la sortie par rapport à l'entrée on aura :

(Système du premier ordre), puisque le dénominateur est un polynôme du premier degré en p, où* p est l'opérateur de Laplace.