II.7. Performances d'un
système asservi
Un système dans son fonctionnement est
caractérisé par un certain nombre de paramètres qu'il
faut :
1. Prévoir (au minimum)
2. Corriger (au mieux)
Un système performant doit être :
- Stable (la stabilité), obligatoirement, sinon on ne
peut l'asservir
- Précis (la précision)
- Rapide (la rapidité)
- Ayant un dépassement nul ou limité.
II.7.1. Stabilité des
systèmes linéaires asservis
Un système est stable si et seulement si à tout
signal borne en entrée, correspond un signal borné en sortie. En
automatique, on définira la stabilité par une des propositions
suivantes : Un système linéaire est stable si est le
seulement si:
- lorsque sa réponse à un échelon prend une
valeur finie en régime permanent,
- lorsque sa réponse à une impulsion tend vers
0,
- lorsque sa réponse à une sinusoïde est une
sinusoïde d'amplitude finie.
Dans la pratique, on exige que le signal de sortie converge
effectivement vers une valeur finie.
D'une manière générale, aucun signal dans
la boucle de régulation ne doit osciller ou tendre vers l'infinie.
Un système asservi est stable si et seulement si sa
fonction de transfert en boucle fermée ne possède aucun
pôle à partie réelle positive.
II.7.1.1. Critère
mathématique de stabilité
Ce système possède un certain nombre
d'inconvénients :
- Sérieux souci pour des polynômes
paramétrés (contient plusieurs paramètres)
- Il est trop binaire et ne laisse pas place à la
notion de la marge de stabilité.
II.7.1.2. Critère
algébrique de ROUTH
Pour savoir si les pôles d'une fonction de transfert
sont à parties réelles négatives, on peut les calculer.
Mais pour des polynômes de degré supérieur à 2, la
résolution devient difficile. Le critère de Routh est un
critère algébrique qui permet de savoir si les racines sont
toutes à partie réelle négative (donc si le système
est stable) sans avoir à calculer ces pôles.
1.1. Equation caractéristique
Dans le cas de l'étude de la stabilité en BF,
l'équation caractéristique est :
 (2.28) (2.28)
Avec :
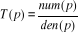 (2.29) (2.29)
Que l'on peut mettre sous la forme :
 (2.30) (2.30)
 (2.31) (2.31)
II.7.1.3. Tableau de
Routh
On forme le tableau suivant :
 (2.32) (2.32)
Avec :
 (2.33) (2.33)
 (2.34) (2.34)
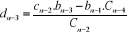 (2.35) (2.35)
Ce tableau est à former jusqu'à ce que l'on ait n
lignes.
Le critère de Routh est le suivant : Si tous les termes
de la première colonne sont strictement positifs, le système est
stable. S'il y a c changements de signes dans la première colonne,
l'équation caractéristique a c racines à parties
réelles positives (et le système est instable).
| 


