III- Comman de vectorielle de la machine asynchrone
Le contrôle vectoriel de la machine asynchrone
construite ci haut (1.15), consiste principalement à commander en
régime dynamique et séparément (de façon
découplée) le flux et le couple
comme c'est le cas (naturellement) pour une machine à courant continu
(excepté de type série).
Le schéma général de principe est le suivant
:
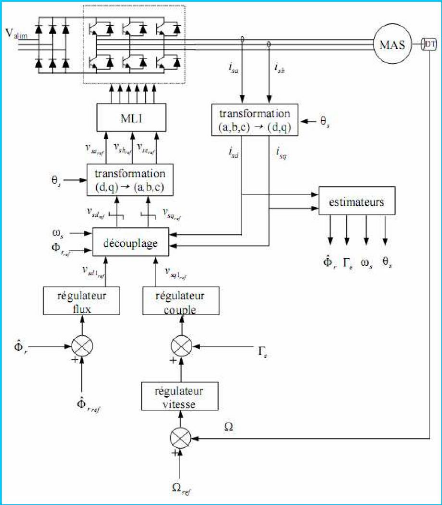
Figure 1-4 : Schéma de principe d~une
comman de vectorielle ( directe) [12]
111.1- Choix de la stratégie de comman de
Le contrôle vectoriel consiste donc à choisir un
système d'axe (d ,q ), de
façon à régler le flux par une composante du courant (
Isd ) et le couple par l'autre composante (
Isq ).
Ainsi, on peut construire une loi de commande assurant le
découplage du couple et du flux permettant d'obtenir des fonctionnements
comparables à ceux de la MCC (excepté de type série).
Cette régulation de flux statorique ou rotorique
(orienté suivant l'un des axes d et q) peut être soit directe soit
indirecte.[4]
· Contrôle directe : le flux est
régulé par une contre-réaction. Il doit donc être
mesuré ou estimé.
· contrôle indirect : le flux
n'est ni mesuré ni reconstruit. Il est fixé en boucle ouverte.
Ainsi, les tensions ou courants assurant l'orientation du flux et le
découplage sont évalués à partir d'un modèle
de la machine en régime transitoire.
Nous adopterons dans ce projet une stratégie de
commande indirecte par orientation du flux rotorique avec capteur de position
ou de vitesse au rotor, nécessaire pour effectuer les changements de
coordonnées. Elle est plus simple que la commande directe mais les
résultats obtenus sont de performances plus
faibles.[5]
111.2- Choix de l'orientation du flux
La suite du raisonnement consiste à fixer l'orientation du
flux. Trois possibilités se présentent :
- Flux statorique : ø sd = ø
s et øsq = 0 (1.16)
- Flux d'entrefer : ø ed = øe
øeq = 0 (1.17)
- Flux rotorique : ø rd = ø
r et ørq = 0 (1.18)
L'orientation du flux statorique et du flux d'entrefer ne
donne pas de bonnes performances par rapport à l'orientation du flux
rotorique qui permet d'obtenir un couple important tout en nécessitant
une adaptation des paramètres rotorique (qui varient avec la
température et la fréquence)[4]. L'orientation
du flux rotorique permet aussi d'éliminer l'influence des
réactances des fuites rotorique et statorique et est ainsi la plus
utilisée.
Nous choisissons donc d'orienter le flux rotorique suivant
l'axe d du repère (d , q ) de Park.
D'où l'appellation classique « Commande vectorielle
à flux rotorique orienté. » (en réalité, c'est
l'axe d qui est orienté sur le flux rotorique). Ainsi, les
conséquences (ø rd = ø r
et ørq = 0 ) sont injectées dans les
équations du modèle pour obtenir les lois de commande et
d'autopilotage ci-dessous :
· Loi de commande par orientation de flux
rotorique
Elle est obtenue par la dernière équation du
système d'état (1.15) :
0 = MR - ù ø soit :
r I
sq r rdLr
· Loi d'autopilotage
Il s'agit simplement de la loi de fonctionnement de la machine
asynchrone, mais en tenant compte de la loi d'orientation ci-dessus.
Nous avons donc : ùs =
ùr + ù . (1.20)
Et avec ùr = I
sqet ù = 1Ù , nous obtenons :
ôrø rd
|
Isq
ùs = +1Ù ô
r ø
rd
|
(1.21)
|
|
| 


