Commande vectorielle à flux rotorique orienté de la machine asynchrone:simulation et expérimentation

111.3- Calcul de l'angle ès des transformations

Pour obtenir l'orientation choisie, il faut calculer la pulsation statorique ù_s à intégrer pour obtenir l'angle è_s nécessaire aux transformations de coordonnées.

On obtient donc à partir du calcul précédent (1.22), l'angle de transformation :

= Jùsdt =J(

^sq +1Ù )dt

ô r ørd

è_s

(1.22)

On peut ainsi à partir de la mesure de la vitesse (angulaire) mécanique, estimer la pulsation statorique et par conséquent l'angle des transformations.

Le couple électromagnétique devient avec ø r = MImr :

M ²

M ( ) ( mr sq ) ( ) _s [ mr sq ]

I = p I I p 1 L I I

ø = - ó

sq rd

L_r

C _em= p

L_r

(1.23)

Le courant magnétisent I_mr étant à la constante de temps rotorique près, l'image du courant _Isd . Le courant _Isd permettra de fixer le flux ø_r et le courant _Isq servira à piloter le

couple électromagnétique.

Un schéma de principe d'une commande vectorielle indirecte à flux orienté, intégrant les

différents blocs de calcul des lois est le suivant :

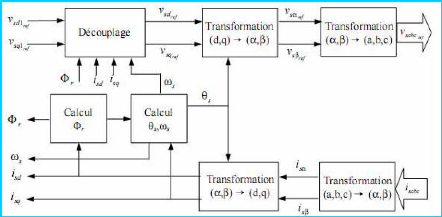
Figure 1-5 : Schéma de principe d'une comman de vectorielle in directe a orientation de flux [12]

111.4- Choix du mode d'alimentation

Pour ce type de commande, l'alimentation de la machine est faite par un onduleur de courant ou de tension selon les besoins.

· Alimentation en courant Pour une alimentation en courant, les variables de commande sont _Isd ^et _Isq . Mais la

source de courant est lourde et chère à cause des inductances de lissage. Ce mode d'alimentation est beaucoup plus réservé aux applications de très fortes puissances où la forme du courant est particulièrement prise en compte (pour réduire les ondulations de couple).

· Alimentation en tension Dans ce cas, les variables de commande sont _Vsd et V_sq . Les onduleurs de tension qui

ne nécessitent pas d'inductance lourde et coûteuse indispensable pour réaliser une source de courant, sont beaucoup préférés et utilisés en traction électrique (TGV transmanche, voiture électrique,...) [5].

Nous choisissons donc pour la machine une alimentation en tension et contrôlée en courant. De tous les modèles courants, nous choisissons le modèle ayant pour:

- variables d'état : Isd , _Isq , _ørd ^et ørq .

- variables de commande : Vsd et V_sq .

Ce modèle qui est utilisé pour orienter le flux rotorique ø_r [5] est celui décrit par le système d'équations d'état (1.15) précédent.

111.5- Synthese du modele final

En injectant les expressions de l'orientation du flux rotorique (ø rd = ø _r et ørq = 0 ) dans les équations des tensions (1.14), on obtient :

RrIrq

0

dø

r

MIrdd

Isd

I MI

+

sq rq

L_r

I rd

MIsdd

L_r

Irq q+#177;MIsqq

Vsd

^Vsq

R_s

0

Isd

R_r

ù

ù

s sq

ø

øsd

øsq

ør

0

RsIsq

s sd

ø

~

~

L

+

dø

sd

dø

sq

+ +

dt

+

dt

+

ù

r ør

~

~~

L

dt

I rd

avec

L_s

L_s

(1.24)

Et le couple électromagnétique : ( sq rd )

C = p I ø

^em L r

M

(1.25)

Le flux rotorique peutêtree obtenu par la relation :ø _rr = MI_mr . (1.26)On définit ainsi le courant magnétisant I mr,== et on obtient de la troisième équation duu

(1.22), combinée à celle des flux :

d

ø M 1 dI 1 - 1

rd mr

= I ø

sd - =

r ? I I

sd

dt

mr

ô r ôr

dt ô ô

devient : pI _mr ô r = I sd - I _mr .

1

Ce qui donne : sd

I = I

^mr 1

+ pô_r

r r

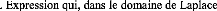
(1.27)

Relation montrant que les deux grandeursI_mr. et I_sd sontégales,, enrégimee permanent.

Apres combinaison deséquationss du (1.22), leséquationss des tensions statoriquesen n d et qs'écriventt :

R_s

Isd

+

dø/

dtt

MM

rr

+

Lrr

MLr) 2 dI sd M ù _s- _Lr )I

sq

~ _-M² ~
~ ~

~ L r ~

R_s

I _sq + L_s

(1.28)

~

~~ ~ ~ ~

Vsd

^Vsq

L

+

MM

Lrr

~ -M 2 ~

~ L I ~

s sd

~ L r ~

:

dt

+ ù_s

dIsq

1

dans les

Dans le domaine de Laplace, en remplaçanø _rr = MImrr , ave sd

I = I

^1
1

mr d++pôr,

équations ci-dessus, on obtient :

2

M

_M2

+L s - ^M Isd -ùL s - ML:1I

L_r^sq

~ -M 2 ~

~ L I ~

s sd

~ L r ~

:

~

~~ ~ ~ ~

Vsd

Isd

R_s

L

RsIsq

^Vsq

22

MM

pImrr

22

(1.29)

MM

mrr

LL

Lrr

L_r

)pI

sq

~ ~
~

+

L_s

+ ù_s

On peut constateràa partir de ceséquationss que lesystèmee des deux axes est ^fortementcouplée : chacune des composantes (entrées)V_sdd et V_sq de la tension influenceàa la fois les
courants (sorties) I_sd etI_sqq . Pour contourner ceproblèmee et pouvoircontrôlerr le flux

. Expression qui, dans le domaine de Laplace

indépendamment du couple, nous allons transformer ce système multi variable (deux entrées et deux sorties couplées) en deux systèmes mono variables (une entrée, une sortie).