Commande vectorielle à flux rotorique orienté de la machine asynchrone:simulation et expérimentation

1.2- Modele diphase de la machine

D'après le théorème de Blondel, deux enroulements en quadrature suffisent pour créer un champ tournant. Donc le champ tournant crée par un système d'enroulements triphasées (trois bobines) équilibrées peut également être crée par le système diphasé (deux enroulements en quadrature) équivalent.

1.2.1- Transformation de Clarke ou de Concordia

Passage du systeme triphase fixe au systeme diphase fixe

Les transformations de Clarke et de Concordia permettent (l'une ou l'autre) de passer d'un repère à trois axes équilibrés (triphasé) abc à un repère à deux axes en quadrature (diphasé) áâ . Ce qui est très intéressant puisque l'objectif de la commande vectorielle est de parvenir à commander séparément les deux grandeurs flux et couple qui seront chacune, associée à un axe.

L'objectif de toute commande de machine étant le transfert maximum de puissance (entre la machine et sa charge), nous choisissons pour la suite la transformation de Concordia qui conserve la puissance et non les amplitudes par rapport à celle de Clarke qui ne conserve que les amplitudes et pas la puissance. Cette transformation se fait en appliquant au système triphasé X , la matrice T_{3 2} de Concordia comme suit :

1

=

2

-

-

2

2

3

2

3

0

T3 2

[

x_a

T3 2

x_á

1 ~ i

xb

[

x_â

x_c

1 ~

~

li

soit [ x_áâ ] = T3 ₂ [ _xabc ] ; avec

(1.4)

3 1

1

2

1 ~ ~ ~ ~ ~

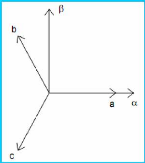
Figure 1-2 : Illustration du passage de abc a áâ [¹⁴]

I.2.3- Transformation de Park

Passage du repere fixe ( á , â) au repere tournant (d , q )

Toujours dans le but de rendre compte au mieux de la réalité, il est nécessaire de travailler dans un repère tournant, puisque le rotor de la machine est en mouvement.

Grâce à la transformation de Park qui n'est rien d'autre qu'une rotation d'angle è (angle
électrique correspondant à la position choisie pour la transformation), il est possible de passer
du repère fixe (á ,â ) à un repère tournant (d , q ) dit de Park, qui peut ensuite être associé

soit au stator, rotor ou champ tournant.

La transformation se fait ainsi en appliquant au système diphasé X , la matrice de rotation

R (è) telle que :

)

x_á

x d

1

1

1

R (è

1 1

_1

x_â

x_q

[

[

soit [ x_dq ] = R ( è ) [ x _áâ ] ; avec ~~

~ cos è sin è ~

R( )

è = (1.5)

~~ - sin cos

è è

Figure 1-3 : Illustration de la transformation de Park (de áâ a dq ) [12]

Le système triphasé X dans le repère ( a , b , c ) peut également et simplement être représenté par son équivalent dans le repère (d , q ) de Park par application de la matrice P(è) de Park telle que :

(1.7)

)

x_a

P(è

x d

~ ~ ~

xb

[

x_q

x_c

[

1 ~

~

LI

soit [ x _dq ] = P(è)[ x_abc ] ;

~ 2 ð 2 ð

cos ~ - ~ ~

cos ~~ ~~ ~ + ~

~ è è cos ~~ è ~~ ~

2 3 3

avec P ( è ) = ~ ~ (1.6)

3 ~ ~ - 2 ð ~ ~ ~

- - è ~~ - ~ + 2 ð

sin è sin

~ ~~ sin ~~ è ~~ ~

~ 3 3 ~

Dans la suite, nous utiliserons cette transformation directe qui rend les différentes grandeurs constantes.

( )

ù ã

t +

~ + - 2 ð ~

~~ ù ã ~~

3

t

~ + + 2 ð ~ ~~ ù ã

t ~~

3

v _sa= V

v sb V

v _sc= V

cos

cos

2. cos

2.

2.

L

Pour un système de tensions statoriques _vabc triphasé équilibré telle que :

La transformation est :[v _dq ] = P(è)[ _vabc ] et le développement du calcul fournit :

V_sd = V 3 cosã et V_sq = -V 3 sinã (1.8)