1.4.4 La classification spatiale
La tâche de classification consiste à attribuer un
objet à une classe parmi un
ensemble donné de classes. Cette
attribution est faite sur la base des valeurs
d'attribut de cet objet. Dans
la classification spatiale les valeurs des attributs des
> 1 Km
Banlieue
Ville
Riche
Pauvre
Village
= 1 km
Villas Baraque
Type de maison
Riche
Type de la région
Pauvre
Pauvre
Distance par rapport à une firme
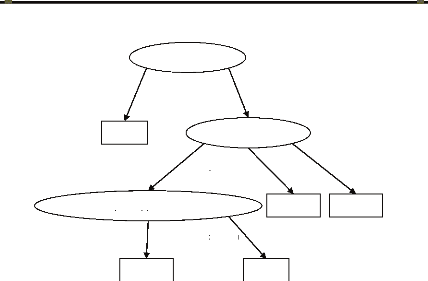
Figure 1-2. Arbre de décision pour la
classification des régions en riches vs pauvres
objets voisins d'un objet peuvent également être
pertinents pour sa classification, donc elles doivent être prises en
considération (Azimi and Delavar 2007).
Cette tâche est réalisée par
l'apprentissage supervisé qui, à partir de classes fournies
partiellement en extension (un échantillon de la base de
données), induit une description en intention (un modèle
générique qui relie les attributs) permettant de classer les
prochaines données (Aufaure, Yeh et Zeitouni 2000).
Exemple
Supposons que nous souhaitons classifier les régions
d'une wilaya en riches versus pauvres. Pour ce faire, il faut identifier les
facteurs importants liés à l'espace qui détermine la
classification d'une région. Beaucoup d'attributs peuvent
révéler intéressants pour cette classification, comme, le
type de la région (village, banlieue, ville), type de maison qu'elles
contiennent (villas, Baraques), et être à proximité d'une
firme. Un modèle de classification est représenté sous
forme d'un arbre de

classification (voir Figure 1-2)1 ou d'un ensemble de
règles, appelées aussi arbre de décision et règles
de décision respectivement.
1.4.5 L'analyse des tendances spatiales
La tendance spatiale est un changement régulier d'une
ou de plusieurs attributs non-spatiales lors du déplacement en dehors
d'un objet donné (Azimi and Delavar 2007).
Les techniques souvent utilisées pour l'analyse de
tendances spatiales sont la régression et l'analyse de
corrélations.
Exemple
Analyser la tendance du taux de chaumage selon la distance par
rapport à une métropole ou une capitale, ou la tendance du
changement du climat ou de la végétation selon la distance par
rapport à la côte.
1.4.6 L'analyse des cas singuliers
Les cas singuliers ou encore appelés valeurs aberrantes
et extrêmes (outliers en anglais) sont des objets qui ne
respectent pas le comportement général ou le modèle de
données (Han et Kamber 2006).
Shekhar et al (2004) définissent un cas singulier
spatial comme un objet spatialement référencé dont les
valeurs des attributs non-spatiaux sont inconsistants avec celles des autres
objets à l'intérieur d'un certains voisinage spatial.
Exemple
Un taudis (gourbi) dans un cartier de villas est
considéré comme un objet spatial aberrant en se basant sur
l'attribut non spatial «type de maison ».
1 Cet exemple est imaginaire, c.à.d. il ne
représente pas une vraie étude sur des données
réelles.

Nous avons présenté dans cette section des
méthodes d'extraction de pattern. Cependant la validité des ces
patterns n'est pas un but facile à atteindre. L'application triviale des
tâches du data mining peut conduire à de faux résultats. En
effet, les tâches du data mining ne sont pas « stand-alone »
mais elles doivent s'exécuter au sein d'un processus bien
déterminé, ce qui est l'objet de la section suivante. Une des
étapes de ce processus est ensuite l'entrée vers le domaine de la
désambiguïsation des toponymes.
| 


