8.2.4 Modes de
représentation des systèmes d'élevage
Dans ses travaux de thèse, Bernard mentionne que la
conception d'un modèle de système d'élevage
nécessite de faire une représentation qui permet de mieux
appréhender le phénomène étudié [Bernard,
2010]. Ainsi, une première représentation par Landais qui permet
l'identification des éléments et des interactions à
prendre en compte pour comprendre le fonctionnement d'un système
d'élevage, conduit à un schéma général de
départ extrêmement simple (Figure 2.2).
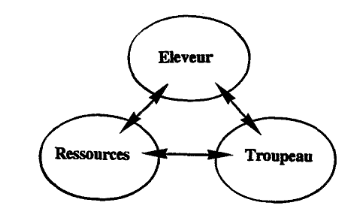
Figure 2.2 : Le modèle de base de la
structure d'un système d'élevage [Landais, 1993]
Parti de cette représentation, l'on rencontre diverses
autres représentations de SE développées dans la
littérature. Parmi ces représentations, figure un schéma
proposé originellement par Lhoste puis repris et complété
par Landais. Cette conception, dont une version est proposée en figure
2.3, définit le système d'élevage comme un système
piloté à trois pôles à savoir :
Ø Le pôle « éleveur »,
identifié comme le pôle principal. C'est au sein de ce pôle
que Landais situe une dimension « travail » et il souligne que «
différentes études ont montré l'importance que prend ce
facteur (le travail) dans les motivations et les choix des éleveurs, et
il n'est plus possible de le négliger ».
Ø Le pôle « troupeau » qui peut
être vu comme un agrégat dont les caractéristiques
résultent de la somme des individus qui le composent ou bien comme une
véritable entité avec ses propres règles de
fonctionnement.
Ø Le pôle « territoire » où se
situe la dimension spatiale. Le « territoire » ne doit pas être
réduit à des surfaces fourragères exploitées, mais
« doit être perçu comme un milieu structuré, support
contrasté (dans l'espace et dans le temps) de ressources et de
contraintes » [Landais & Bonnemaire, 1996].

Figure 2.3 : Schéma
développé du système d'élevage : pôles et
interfaces [Lhoste, 1984]
8.2.5
Méthodes et techniques de modélisation des SE
Deux méthodes sont largement dominantes pour la
modélisation des systèmes d'élevage : Optimisation et
Simulation.
8.2.5.1
Optimisation
Les modèles basés sur des techniques
d'optimisation sont les modèles où le fonctionnement du
système est basé sur un ou plusieurs objectifs explicites qui est
(sont) sensé(s) refléter le comportement du preneur de
décision ou ses objectifs. Les modèles d'optimisation relatifs
aux systèmes d'élevage visent à optimiser certaines
pratiques agricoles ou stratégies (gestion) ou à identifier un
système optimal, le plus souvent dans un but purement économique,
parfois technique [Pacaud & Cournut, 2007].
Parmi les techniques de mise en oeuvre des modèles
d'optimisation, deux principales restent dominantes [Pacaud & Cournut,
2007] :
Ø La programmation linéaire qui est la plus
fréquente dans les modèles des systèmes d'élevage,
implique que la fonction objectif et les contraintes évoluent de
manière linéaire ;
Ø La programmation dynamique qui admet qu'une solution
optimale se compose nécessairement de sous-solutions optimales.
Stonehouse et al. [Stonehouse & al., 2002]
caractérisent les modèles d'optimisation comme étant
proches du mode de décision de l'agriculteur, permettant la prise en
compte de contraintes variées, particulièrement adaptés
à l'évaluation de politiques environnementales.
Cros et al. émettent quelques réserves dans
l'utilisation de l'optimisation dans les questions de stratégies de
gestion des exploitations agricoles dans le sens où i) il n'y a
généralement pas une seule solution optimale qui répond
à un problème particulier dans la gestion « car
l'efficacité d'une solution dépend de contraintes
spécifiques et du jugement subjectif de l'agriculteur » et ii) la
gestion d'un système de production agricole est
généralement trop complexe pour être
représentée de manière pertinente par l'optimisation et la
nécessité de simplifier la représentation des
stratégies a pour conséquence leur impossibilité de
réalisation dans la pratique [Cros, Duru & al., 2004]. De plus, les
modèles d'optimisation spécifient systématiquement une
hypothèse de comportement, ce qui les différencie des
modèles de simulation [Weersink, Jeffrey & al., 2002].
| 


