3.7. Constance des taux instantanés de transition
Hypothèse
Nous supposons les taux instantanés de transition
constat à chaque âge, c.à.d. quels que soient l'âge x
entier et 0=t=1, les identités suivantes
(3.5)
ìah(x+t)= ìah(x),
ìag(x+t)= ìag(x),
ìha(x+t)= ìha(x),
ìga(x+t)= ìga(x),
sont vérifiées.
3.7.1.
Probabilité de transition annuelle
Commençons par estimer t  en fonction des taux. Partons de l'expression suivante : en fonction des taux. Partons de l'expression suivante :
t+Ät  =Pr[ =Pr[  + +  =e0], étant donné que e0,e1,e2 forment un système
complet d'évenement et que pour un evenement ek avec k°{0,1,2}, un
autre événement ej={0,1,2} ne peut se produire qu'en combinaison
avec l'un de ek du système complet. On applique le
théorème de probabilité totale. =e0], étant donné que e0,e1,e2 forment un système
complet d'évenement et que pour un evenement ek avec k°{0,1,2}, un
autre événement ej={0,1,2} ne peut se produire qu'en combinaison
avec l'un de ek du système complet. On applique le
théorème de probabilité totale.
e0= 
ce qui donne:
Pr[  =e0| =e0|  =e0]= Pr[ =e0]= Pr[  =e0| =e0|  =e0]. Pr[ =e0]. Pr[  =e0| =e0|  =e0]+ Pr[ =e0]+ Pr[  =e1| =e1|  =e0] Pr[ =e0] Pr[  =e0| =e0|  =e1]+ =e1]+
[  =e2| =e2|  =e0]. Pr[ =e0]. Pr[  =e0| =e0|  =e2], =e2],
En se référant à (3.2),
Pr[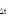  =e0| =e0|  =e0]=t =e0]=t  Ät. Ät.  + t + t  Ät. Ät.  + t + t  Ät. Ät. 
Considérons à présent un âge x
entier, un instant 0<t<1 et un accroissement Ät tel que t+
Ät<1. Nous pouvons alors écrire en se référant
à (3.4)
t+Ät   = t = t  (1-( ìah(x)+ ìag(x)) Ät)+ t (1-( ìah(x)+ ìag(x)) Ät)+ t  ìha(x) Ät+ t ìha(x) Ät+ t  ìga(x) Ät+o(Ät) ìga(x) Ät+o(Ät)
avec o(Ät) :notation de Landau, une fonction
arbitraire de Ät tel que   =0 , ou Ät est un infiniment petit d'ordre supérieur
à Ät. =0 , ou Ät est un infiniment petit d'ordre supérieur
à Ät.
Ceci donne, t+Ät   = t = t  -(( ìah(x)+ ìag(x)) -(( ìah(x)+ ìag(x))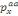  + t + t  ìha(x) + t ìha(x) + t  ìga(x) )Ät+o(Ät) ìga(x) )Ät+o(Ät)
?
  =-( ìah(x)+ ìag(x)) =-( ìah(x)+ ìag(x))  + t + t  ìha(x) + t ìha(x) + t  ìga(x) + ìga(x) + 
Par passage à la limite pour  , on obtient l'équation suivant , on obtient l'équation suivant
  -( ìah(x)+ ìag(x)) -( ìah(x)+ ìag(x))  + t + t  ìha(x) + t ìha(x) + t  ìga(x) (3.6) ìga(x) (3.6)
En procèdent de la même manière on
obtient les équations différentielles suivantes pour les autres
probabilités de transition.
 (3 .7) (3 .7)
Il est simple de résoudre le système
intégro-différentiel de l'ensemble des probabilités de
transition en utilisant une écriture matricielle. En effet introduisant
la matrice Mx reprenant les taux de transition entre paires d'états hors
de la diagonale principale, et l'opposé de la somme des
éléments de la ligne correspondante sur la diagonale
Mx=  
En notant Px(t)=  
Il vient alors que le système (3.7) peut s'écrire
  Px(t)=Px(t) Mx (3.8), Px(t)=Px(t) Mx (3.8),
où la dérivée d'une matrice peut se
comprendre comme la matrice de dérivées. La solution de cette
équation est donnée par la série  
En calculant 3.8 par la méthode de Cox et Miller, en
supposant que Mx possède 3 valeurs propres distinctes  , ,   et et   comme Mx est de rang inférieur ou égal à deux,
l'une des valeurs propres est nécessairement nulle. Le vecteur propre
associé à cette valeur propre est colinéaire au vecteur
(1, 1, 1) T. comme Mx est de rang inférieur ou égal à deux,
l'une des valeurs propres est nécessairement nulle. Le vecteur propre
associé à cette valeur propre est colinéaire au vecteur
(1, 1, 1) T.
Supposons par exemple que   =0, on peut ensuite décomposer Mx comme, =0, on peut ensuite décomposer Mx comme,
Mx=Axdiag (  , ,   et et   ) représente une matrice diagonale 3*3. ) représente une matrice diagonale 3*3.
Dès lors
Px(t)=Ax  + + 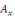 diag ( diag (  , ,   et et   ) )  + +  diag ( diag (  , ,  , ,  ) )  +... +...
=  diag ( diag (  , ,   , ,  ) ) 
=  diag (exp diag (exp 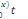 ), exp ), exp  ), exp ), exp  )) )) 
| 


