3.6. Taux instantanés des transitions
3.6.1.
Définitions
Les initiales
« a », « h », « g »
sont utilisés pour rappeler les états
« active », « hospitalisé » et
« grossesse ».
Soit ;
- ìah(x+t)  , le taux instantané de transition de l'état e0 vers
l'état e1 à l'âge x+t. la grandeur
ìah(x+t) quantifie le risque pour un individu
âgé de x+t années d'être hospitalisée suite
à une maladie ou un accident.
- ìha(x+t)  , le taux instantané de transition de l'état e1 vers
l'état e0 à l'âge x+t. la grandeur
ìha(x+t) quantifie le risque pour un individu
âgé de x+t années de sortir de l'hôpital après
y être entré pour une maladie ou un accident.
- ìag(x+t)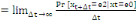  , le taux instantané de transition de l'état e0 vers
l'état e2 à l'âge x+t. la grandeur
ìah(x+t) quantifie le risque pour un individu
âgé de x+t années d'être hospitalisée suite
à une grossesse.
- Ìga(x+t)  , le taux instantané de transition de l'état e2 vers
l'état e0 à l'âge x+t. cette grandeur
ìah(x+t) quantifie le risque pour un individu
âgé de x+t de sortir de l'hôpital après y être
entré suite à une grossesse.
Il est à noter que le taux d'hospitalisation suite
à une grossesse ne dépend que de l'âge et pas de la date de
la dernière entrée à l'hôpital pour une
grossesse.
3.6.2. Lien avec
les probabilités de transition
Soit les probabilités de transition entre les instants
s et t, tel que s<p. On peut exprimer les probabilités de transition
entre les différents états de la manière
suivante :
 (3.2)
Il s'agit respectivement de la probabilité qu'une
assurée active à l'âge x+s le soit également
à l'âge x+t , qu'une assuré active à l'âge x+s
se retrouve hospitalisée à l'âge x+t, qu'une assurée
active à l'âge x+s se retrouve hospitalisée suite à
une grossesse à l'âge x+t, qu'une assurée
hospitalisée à l'âge x+s soit sortie de l'hôpital
à l'âge x+t, qu'une assurée hospitalisé à
l'âgé x+s le soit également à l'âge x+t,...
Ces probabilités fixent les états occupés
aux instants s et t.
3.6.3. Expression
des probabilités de transition sous forme de taux de transition
Le taux de transition peut se voir comme des
dérivées partielles des probabilités de transition par
rapport au temps imparti pour effectuer le parcours requis
 (3.3)
Par conséquence un développement de Taylor
limité au premier ordre donne les expressions suivantes :
 (3.4)
| 
