Etude du modèle de tarification de prime d?assurance maladie par l'approche stochastique (cas de l'hôpital Saint Joseph de Kinshasa)

3.8. Lien avec les probabilités de séjour

3.8.1. Définition

Les probabilités de séjour sont les probabilités d'occuper sans arrêt un état entre les instants s et t. Ces probabilités dans les différent états sont données par

t-s 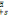=Pr[X_T=e0 pour tout s<T<t /Xs=e0]

= Pr[X_T=e0 et D_T=t-s pour tout s<T<t /Xs=e0]

t-s =Pr[X_T=e1 pour tout s<T<t /Xs=e1]

= Pr[XT=e1 et DT=t-s pour tout s<T<t /Xs=e1]

t-s =Pr[X_T=e2 pour tout s<T<t /Xs=e2]

= Pr[XT=e2 et DT=t-s pour tout s<T<t /Xs=e2]

Avec D_T la durée d'occupation d'un individu dans l'état a,h,g

3.8.2. Expression des probabilités de séjour en fonction des taux des transitions

On peut également exprimer les probabilités de séjour en fonction des taux des transitions. Pour obtenir l'expression de t en fonction des taux des transitions, partons de l'expression suivante obtenu en conditionnant par rapport à l'état occupé par l'assuré entre les instants s et t.

t+Ät = t t.Ät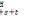 en se referant à (3.4), on peut écrire

t+Ät = t [1-( ì_ah(x+s+t)+ ì_ag(x+s+t))Ät+o(Ät)] en posant

ì_ah(x+s+t)+ ì_ag(x+s+t)= ì_a.(x+s+t)

on a t+Ät = t [1- ì_a.(x+s+t)Ät+ o(Ät)]

ce qui donne t . ì_a.(x+s+t)Ät+

En passant à la limite pour ?0, on obtient l'équation différentielle 

t . ì_a.(x+s+t)

A la condition initiale t=0, ou à =1, l'équation différentiel possède comme solution satisfaisant les conditions initial,

t =exp(- )+ )dô)

on vérifie aussi de la même façon que :

t =exp(- )dô)

t =exp(- )dô)