1.2.3. Les modèles ARIMA.
Nous allons présenter une famille de processus
aléatoires qui sont censés recouvrir une gamme très large
d'évolution possible de séries chronologiques : les processus
autorégressifs et les processus de moyenne mobile.
1.2.3.1. Typologie des modèle AR et MA et ARMA.
1.2.3.1.1. Modèle AR (Auto Régressif) :
1.2.3.1.1.1. Formulation :
Dans le processus autorégressif d'ordre p
l'observation présente yt est générée
par une
moyenne pondérée des observations passées
jusqu'à la p-ième période sous la forme suivante
:
AR (1) : yt = 1 yt-1 + t
AR (2) : yt = 1 yt-1 + 2 yt-2 + t
. . .
AR (p) : yt = 1 yt-1 + 2 yt-2 +
. . . + p yt-p t [3]
où 1, 2 , . . . ,
p sont des paramètres à estimer positifs ou
négatifs, t est un aléa gaussien.
Nous pouvons ajouter à ce processus une constante qui ne
modifie en rien les propriétés stochastiques. L'équation
[3] peut aussi s'écrire à l'aide de l'opérateur
décalage D :

1.2.3.1.1.2. Caractéristiques des
corrélogrammes :
Il est démontré que le corrélogramme simple
d'un processus AR(p) est caractérisé par une
décroissance géométrique de ses termes de type :
k = k
Le corrélogramme partiel a ses seuls p premiers
termes différents de 0.
1.2.3.1.2. Modèle MA (Moving Average : Moyenne
Mobile) :
1.2.3.1.2.1. Formulation :
Dans le processus de moyenne mobile d'ordre q, chaque
observation yt est générée par une moyenne
pondérée d'aléas jusqu'à la
qième période.
où 1, 2, . . .
, q sont des paramètres pouvant être
positifs ou négatifs et t, est un aléa gaussien.
L'équation [4] peut aussi s'écrire :

Dans ce processus, tout comme dans le modèle
autorégressif AR, les aléas sont supposés être
engendrés par un processus de type bruit blanc. Nous pouvons
interpréter le modèle MA comme étant représentatif
d'une série chronologique fluctuant autour de sa moyenne de
manière aléatoire, d'où le terme de moyenne mobile car
celle-ci, en lissant la série, gomme le bruit créé par
l'aléa.

Il est à noter qu'il y a équivalence entre un
processus MA(1) et un processus AR d'ordre p infini :
1.2.3.1.2.2. Caractéristiques des
corrélogrammes :

Le corrélogramme simple d'un processus MA(q) est
de la forme générale :
our k = 0,1, . . . , q
et k = 0 pour k > q
C'est-à-dire que seuls les q premiers termes du
corrélogramme simple sont significativement différents de 0.
Le corrélogramme partiel est caractérisé par
une décroissance géométrique des retards.
1.2.3.1.3. Modèle ARMA (mélange de
processus AR et MA). 1.2.3.1.3.1. Formulation :
Les modèles ARMA sont donc représentatifs d'un
processus généré par une combinaison des valeurs
passées et des erreurs passées. Ils sont définis par
l'équation :
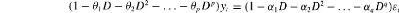
ARMA(p,q) :
Nous avons :
ARMA(1,0) = AR(1) ; ARMA(0, 1) = MA(1). 1.2.3.1.3.2.
Caractéristiques des corrélogrammes
Les corrélogrammes simples et partiels sont, par voie
de conséquence, un mélange des deux corrélogrammes des
processus AR et MA purs. Il s'avère ainsi plus délicat
d'identifier ces processus à partir de l'étude des fonctions
d'autocorrélation empiriques.
Le tableau 3 synthétise les caractéristiques, en
termes de corrélogrammes, des processus AR, MA et ARMA.
1.2.3.1.3.3. Condition d'utilisation :
Les modèles AR, MA, ARMA ne sont représentatifs que
de chroniques :
- stationnaires en tendance ;
- corrigées des variations saisonnières.
| 


