CHAPITRE III :
GENERATEURS PSEUDO-ALEATOIRES
Définition
Soit   un ensemble fini appelé espace d'états, un
générateur pseudo-aléatoires est défini
par : un ensemble fini appelé espace d'états, un
générateur pseudo-aléatoires est défini
par :
  , ,
et l'état s'évolue selon :   , ,  
l'état initial   s'appelle germe ou graine. s'appelle germe ou graine.
Autrement dit un générateur
pseudo-aléatoire est un procédé qui, à partir d'une
initialisation de taille fixée appelée germe ou graine, engendre
de manière déterministe une séquence de très grande
longueur.
Cette séquence consiste à imiter une
séquence de variables aléatoires.
Définition
Une séquence binaire   constituée de constituée de   bits est dite aléatoire lorsque les bits est dite aléatoire lorsque les   bits sont indépendants, imprédictibles et
équiprobables. bits sont indépendants, imprédictibles et
équiprobables.
Un générateur de nombres
pseudo-aléatoires et un générateur de bits
aléatoires ont pour buts de générer une séquence
de mots aléatoires. Les mots appartiennent à l'alphabet fini   Dans le cas d'un générateur de bits aléatoires,
l'alphabet est de dimension 2 c'est.-à-dire. Dans le cas d'un générateur de bits aléatoires,
l'alphabet est de dimension 2 c'est.-à-dire.  
On distingue plusieurs générateurs
pseudo-aléatoires tels que Générateur à congruence
linéaire, Générateur
carré-médian, Générateur à
congruence additive, Générateur de type «
multiplication avec retenue », Générateur de Blum-Blum-Shub
ou Générateur quadratique etc....
III.1. Exemples de quelques
générateurs pseudo-aléatoires
1. Générateur à congruence
linéaire
Le générateur à congruence
linéaire est un algorithme inventé par Lehmer en 1948. C'est une
suite définie par la relation suivante :

où   est appelé multiplicateur, est appelé multiplicateur,   est l'incrément, et est l'incrément, et   est le module (le maximum plus un des nombres de la suite). La suite
est initialisée par le germe est le module (le maximum plus un des nombres de la suite). La suite
est initialisée par le germe   . Tous ces nombres sont positifs. . Tous ces nombres sont positifs.
Pours avoir une période maximale, les paramètres
suivants doivent être respecté avec   non nul : non nul :
 - -  et et   doivent être premiers entre eux doivent être premiers entre eux
 - -  doit être multiple de doit être multiple de   , ,   nombre premier diviseur de nombre premier diviseur de  
Exemple :  
Avec  , la suite est : , la suite est : 
2. Générateur
carré-médian
Le générateur carre-médian
est construit de la manière suivante : on
élève au carré un nombre de 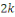  -chiffres et on prend les -chiffres et on prend les  -chiffres du milieu du produit (de -chiffres du milieu du produit (de   chiffres). Il fut historiquement l'un des premiers
générateurs utilisés mais c'est un très mauvais
générateur ; si l'on tombe sur zéro tous les autres termes
de la suite seront nuls et de manière générale sa
période est trop courte. chiffres). Il fut historiquement l'un des premiers
générateurs utilisés mais c'est un très mauvais
générateur ; si l'on tombe sur zéro tous les autres termes
de la suite seront nuls et de manière générale sa
période est trop courte.
Exemple :
|
12
|
14
|
19
|
36
|
29
|
84
|
5
|
2
|
0
|
0
|
|
0144
|
0196
|
0361
|
1296
|
0841
|
7056
|
0025
|
0004
|
0
|
0
|
3. Générateur à congruence
additive
Le générateur à congruence additive est
défini de la manière suivante :
Soient   des entiers naturels, pour des entiers naturels, pour  
 
Pour   on obtient la suite de Fibonacci. on obtient la suite de Fibonacci.
Cette méthode a deux inconvénients :
1. Il nécessite de stocker   nombres. nombres.
2. Si 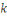  est petit les nombres présentent une forte
corrélation. est petit les nombres présentent une forte
corrélation.
4. Générateur Blum-Blum-Shub
Définition
L'ensemble des résidus quadratiques   est noté par est noté par   et l'ensemble des non-résidus quadratiques et l'ensemble des non-résidus quadratiques   est noté par est noté par  
Définition
Un entier de Blum est un produit de deux premiers distincts
dont tous deux congrus à 3 modulo 4.
Proposition
Soit   un entier de Blum et soit un entier de Blum et soit   un carrée de un carrée de   alors alors   possède quatre racines carrées dont une (et une
seule) est un carrée de possède quatre racines carrées dont une (et une
seule) est un carrée de   . Cette racine est appelée racine principale de . Cette racine est appelée racine principale de  
Preuve
Comme le nombre de racines carrées de   est quatre, on peut écrire que ces racines carrées
sont : est quatre, on peut écrire que ces racines carrées
sont :   dans dans   (qui s'identifie à (qui s'identifie à   grâce au théorème des restes chinois), seul le
couple formé par les deux racines principales de grâce au théorème des restes chinois), seul le
couple formé par les deux racines principales de   modulo modulo   et modulo et modulo   est un carré modulo est un carré modulo 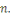 
Définition
Le générateur Blum-Blum-Shub est définit
de la manière suivant :
Soit   un entier de Blum tel que un entier de Blum tel que   et et  
On choisit un nombre   d'une manière aléatoire tel que d'une manière aléatoire tel que   , alors le germe de la suite est calculé par : , alors le germe de la suite est calculé par :   . Et les autres termes de la suite sont définis par : . Et les autres termes de la suite sont définis par :

Exemple
Soit 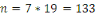  et et   . Alors . Alors   . Les autres termes sont : . Les autres termes sont :         . La sortie en bit : 1, 0, 0,1, avec . La sortie en bit : 1, 0, 0,1, avec   . .
| 


