III.2.
Générateurs cryptographiquement sûrs
Du point de vue de la formalisation de la
sécurité d'un générateur pseudo-aléatoire,
il faut d'une part définir le problème de sécurité,
d'autre part il faut définir ce qu'est l'attaque. Un attaquant est
considéré comme un algorithme réalisable qui sort un
résultat relatif au problème de sécurité
posé. La notion d'algorithme réalisable est extrêmement
importante car comme on travaille souvent sur des situations finies on peut
décrire théoriquement des algorithmes qui cassent la
sécurité des systèmes. Mais ces algorithmes ne sont pas
réalisables en pratique à cause de la durée des calculs.
On cherche donc à assurer la sécurité calculatoire.
Nous allons utiliser le générateur de
Blum-Blum-Shub qui est cryptographiquement sûr.
Définition
Soit   un paramètre, appelé paramètre de
sécurité. un paramètre, appelé paramètre de
sécurité.
Définition
Soit   une fonction en une fonction en   telle que telle que   Un générateur pseudo-aléatoire est une fonction Un générateur pseudo-aléatoire est une fonction
  calculable en temps polynomial en calculable en temps polynomial en   de de   dans dans  . .
Lorsque nous composons la distribution uniforme sur   avec avec  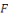 , nous obtenons une distribution sur , nous obtenons une distribution sur   appelée la distribution induite par appelée la distribution induite par  . .
Définition
Soit   un générateur pseudo-aléatoire et un générateur pseudo-aléatoire et   . Un . Un   -distingueur pour -distingueur pour   est un algorithme est un algorithme   probabiliste polynomial probabiliste polynomial   tel que tel que

où   signifie que les bits signifie que les bits 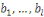  sont choisis selon la distribution induite par sont choisis selon la distribution induite par   et et   qu'ils sont choisis selon la distribution uniforme. qu'ils sont choisis selon la distribution uniforme.
Définition
Un générateur pseudo-aléatoire  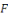 est dit cryptographiquement sûr s'il n'existe d' est dit cryptographiquement sûr s'il n'existe d'   -distingueur pour -distingueur pour   que pour des fonctions que pour des fonctions   négligeables (par rapport au paramètre négligeables (par rapport au paramètre  
III.3. Extrapoleurs
Définition
Soit   un générateur pseudo-aléatoire, un générateur pseudo-aléatoire, 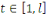  un entier, et un entier, et   . On note . On note   des bits choisis suivant la distribution induite par des bits choisis suivant la distribution induite par   sur sur   . Un extrapoleur d'ordre . Un extrapoleur d'ordre   pour pour   d'avantage d'avantage   est un algorithme probabiliste polynomial calculant le bit est un algorithme probabiliste polynomial calculant le bit   en fonction des précédents en fonction des précédents   avec probabilité avec probabilité 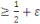  . .
Ainsi à partir d'un extrapoleur   d'ordre d'ordre   et d'avantage et d'avantage   pour pour   , nous obtenons un , nous obtenons un   -distingueur -distingueur   pour pour   comme suit : comme suit :





La probabilité que   soit égal à soit égal à   vaut au moins vaut au moins   lorsque lorsque   est choisi selon la distribution induite par est choisi selon la distribution induite par  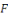 et vaut et vaut   lorsque lorsque   est choisi selon la distribution uniforme. est choisi selon la distribution uniforme.
Théorème de Yao
Un générateur pseudo-aléatoire   est sûr si et seulement si, pour chaque est sûr si et seulement si, pour chaque   entier, il n'existe pas d'extrapoleur pour entier, il n'existe pas d'extrapoleur pour   autres que d'avantage négligeable. autres que d'avantage négligeable.
Preuve
D'après la construction de distingueur à partir
d'un extrapoleur,   ne peut être sûr que si tout extrapoleur n'est que
d'avantage négligeable. ne peut être sûr que si tout extrapoleur n'est que
d'avantage négligeable.
Inversement, supposons que   ne soit pas sûr. Pour ne soit pas sûr. Pour  , notons , notons   la distribution sur la distribution sur   selon laquelle les selon laquelle les   premiers bits premiers bits   sont produits par sont produits par   et les autres et les autres   sont choisis uniformément au hasard. Ainsi, sont choisis uniformément au hasard. Ainsi, 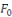  est la distribution uniforme et est la distribution uniforme et   celle induite par celle induite par  . Par hypothèse, il existe un . Par hypothèse, il existe un   -distingueur -distingueur   pour pour   telle que telle que   ne soit pas négligeable, c'est-à -dire ne soit pas négligeable, c'est-à -dire

Donc il existe un   et une fonction et une fonction   pas négligeable tels que pas négligeable tels que

Considérons l'algorithme   suivant : suivant :






Nous allons montrer que   est un extrapoleur d'avantage est un extrapoleur d'avantage   pour pour  
On a tout d'abord   et et
  . .
On a aussi   donc donc

Pour alléger les notations, nous posons   et et   . La probabilité que . La probabilité que   prévoie le bit prévoie le bit   correctement est donnée par correctement est donnée par
 







| 


