III.4 Sécurité du
générateur Blum-Blum-Shub
III.4.1 Problème de la
résiduosité quadratique
Le problème de la résiduosité quadratique
est comme suit : étant donné un nombre  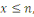 il faut déterminer si il faut déterminer si   est un carré modulo est un carré modulo   ou non. ou non.
Lorsque   un premier, le problème sera résolu en temps polynomial
en la taille de un premier, le problème sera résolu en temps polynomial
en la taille de   par le calcule du symbole de Legendre par le calcule du symbole de Legendre   Puisqu'on sait que Puisqu'on sait que   est un résidu quadratique modulo est un résidu quadratique modulo   si et seulement si son symbole de Legendre est 1. si et seulement si son symbole de Legendre est 1.
Lorsque   est un nombre composé dont on ne connait pas la factorisation,
aucun algorithme polynomial en la taille de est un nombre composé dont on ne connait pas la factorisation,
aucun algorithme polynomial en la taille de   sera disponible pour résoudre le problème de la
résiduosité quadratique. sera disponible pour résoudre le problème de la
résiduosité quadratique.
Supposons que   où où   et et   deux premiers distincts. Si la factorisation de deux premiers distincts. Si la factorisation de   est connue alors le problème de la résiduosité
quadratique se résout en temps polynomial en cherchant tout simplement
si est connue alors le problème de la résiduosité
quadratique se résout en temps polynomial en cherchant tout simplement
si   et et   sont des résidus quadratiques par le calcul de leurs symboles de
Legendre. Mais lorsqu'on ne connait pas la factorisation de sont des résidus quadratiques par le calcul de leurs symboles de
Legendre. Mais lorsqu'on ne connait pas la factorisation de   ,il sera impossible de résoudre le problème en temps
polynomial. ,il sera impossible de résoudre le problème en temps
polynomial.
Un autre problème s'oppose à savoir
l'extraction d'une racine carrée modulaire : sachant qu'un nombre
  est un résidu quadratique est un résidu quadratique   , comment déterminer un nombre , comment déterminer un nombre   tel que tel que  
Nota
Soit   un entier de Blum, un entier de Blum,   un élément de symbole de Jacobi 1 et un élément de symbole de Jacobi 1 et   son carré modulo son carré modulo   On sait que On sait que   , et possède 4 racines carrées dont deux ont pour symbole
de Jacobi 1 : , et possède 4 racines carrées dont deux ont pour symbole
de Jacobi 1 :   et et   . Une et une des deux valeurs . Une et une des deux valeurs   et et   est dans est dans   En outre En outre   et et   ont des parités différentes. Autrement dit, si on
disposait d'un algorithme capable de déterminer avec une
probabilité de succès non négligeable, à partir de ont des parités différentes. Autrement dit, si on
disposait d'un algorithme capable de déterminer avec une
probabilité de succès non négligeable, à partir de
  quelle est la parité de la racine carrée qui est
elle-même un carré, on pourrait déterminer avec la
même probabilité de succès si quelle est la parité de la racine carrée qui est
elle-même un carré, on pourrait déterminer avec la
même probabilité de succès si   est un carré ou non. est un carré ou non.
III.4.2 Détails sur la
sécurité du générateur Blum-Blum-Shub
On va noter   l'ensemble des entiers l'ensemble des entiers   de symbole de Jacobi de symbole de Jacobi   valant 1. valant 1.
Les nombres d'éléments de   est donné par : est donné par :
 
Et aussi 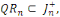  alors alors  
Comme   est un entier de Blum, par conséquent l'application est un entier de Blum, par conséquent l'application   de de   dans lui-même définie par dans lui-même définie par   est une bijection. est une bijection.
Soit   la taille de l'entier la taille de l'entier   qui servira de paramètre de sécurité. On dispose
d'un algorithme probabiliste polynomial en qui servira de paramètre de sécurité. On dispose
d'un algorithme probabiliste polynomial en 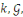  qui étant donné en entrée le paramètre de
sécurité qui étant donné en entrée le paramètre de
sécurité   construit au hasard un environnement de travail, c'est-à-dire
un entier de Blum construit au hasard un environnement de travail, c'est-à-dire
un entier de Blum   de taille de taille   (pour notre cas). Soit la fonction (pour notre cas). Soit la fonction   d'élévation au carrée modulo d'élévation au carrée modulo 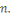  On note On note 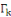  l'ensemble des environnements possibles. l'ensemble des environnements possibles.
Soit   un algorithme probabiliste polynomial en un algorithme probabiliste polynomial en   dont l'entrée est le paramètre de sécurité dont l'entrée est le paramètre de sécurité
  le nombre le nombre   et un élément et un élément   de de   et la sortie un bit et la sortie un bit   dont on souhaite qu'il détermine avec succès si dont on souhaite qu'il détermine avec succès si   est un élément de est un élément de   ou non. ou non.
Considérons les expériences :













L'avantage de l'attaquant   est définie par : est définie par :

Le problème de la résiduosité quadratique
est sûr par l'hypothèse de la difficulté de la
résiduosité quadratique, c'est-à-dire que pour tout
attaquant polynomial   et pour tout entier et pour tout entier     Autrement dit tout attaquant polynomial a un avantage qui est une
fonction négligeable du paramètre de sécurité Autrement dit tout attaquant polynomial a un avantage qui est une
fonction négligeable du paramètre de sécurité  . .
Les algorithmes d'extrapolation
Soit   le paramètre de sécurité, le paramètre de sécurité,   un entier de Blum de taille un entier de Blum de taille   et et   le générateur des nombres pseudo-aléatoire
définie par : le générateur des nombres pseudo-aléatoire
définie par :
  , où pour tout , où pour tout   le calcul de le calcul de  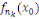 se fait de la façon suivante : se fait de la façon suivante :
1. La bijection  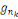 de de   dans lui-même définie par dans lui-même définie par   permet de calculer permet de calculer  
2. Chaque   donne un bit donne un bit  
 3. 3. 
Lemme
Soit   et et   un algorithme probabiliste polynomial qui étant donnés
les bits un algorithme probabiliste polynomial qui étant donnés
les bits 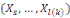 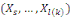 prédit le bit prédit le bit   avec un avantage non négligeable. Alors on fournit en
entrée de cet algorithme probabiliste polynomial, les avec un avantage non négligeable. Alors on fournit en
entrée de cet algorithme probabiliste polynomial, les   bits bits   d'un d'un   , il prédit le bit , il prédit le bit   avec le même avantage non négligeable. avec le même avantage non négligeable.
Preuve
Du fait   est une bijection, la loi de probabilité du terme calculé est une bijection, la loi de probabilité du terme calculé
  est la même que la loi de probabilité du terme tiré
au sort dans est la même que la loi de probabilité du terme tiré
au sort dans   qui sert de germe qui sert de germe  
Pour prouver que le générateur BBS est
sûr, on montrera que s'il existe un extrapoleur probabiliste polynomial
qui prédit le bit   avec un avantage non négligeable, alors, il existe un algorithme
probabiliste polynomial qui possède un avantage non négligeable
pour résoudre le problème de la résiduosité
quadratique. avec un avantage non négligeable, alors, il existe un algorithme
probabiliste polynomial qui possède un avantage non négligeable
pour résoudre le problème de la résiduosité
quadratique.
Soit   un algorithme polynomial probabiliste, dont les entrées sont un algorithme polynomial probabiliste, dont les entrées sont
  et dont l'avantage de prédiction du bit et dont l'avantage de prédiction du bit   n'est pas une fonction négligeable de n'est pas une fonction négligeable de   . Construisons l'algorithme . Construisons l'algorithme   dont les entrées sont ( dont les entrées sont (  où où   et sort un bit. et sort un bit.







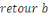

Par le nota précédent, on voit que l'algorithme
  ainsi construit, a un avantage ainsi construit, a un avantage   non négligeable pour le problème de la
résiduosité quadratique. En tenant compte de la difficulté
de la résiduosité quadratique, on conclut que le
générateur Blum-Blum-Shub est sûr. non négligeable pour le problème de la
résiduosité quadratique. En tenant compte de la difficulté
de la résiduosité quadratique, on conclut que le
générateur Blum-Blum-Shub est sûr.
| 


