CHAPITRE IV :
IMPLEMENTATION ET INTERPRETATION DES RESULTATS
Dans ce chapitre nous présentons
l'implémentation de l'algorithme de Blum-Blum-Shub et
l'interprétation des résultats obtenus.
Voici l'algorithme de Blum-Blum-Shub :
Générer   et  
Faire  
Choisir  
Calculer le germe :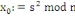  
La séquence est  
Sortie est :  
Nous avons implémenté l'algorithme de
Blum-Blum-Shub en c++ à partir du compilateur DEV-C++.
Voici les codes du programme :
#include <iostream>
#include<conio.h>
using namespace std;
int main()
{
int i,B;
unsigned long long int X,n,p,q,s;
cout<<endl<<"Entrer la valeur de p:";// p un
entier congru à 3 modulo 4
cin>>p;
cout<<endl<<"Entrer la valeur de q:";//q un
entier congru à 3 modulo 4
cin>>q;
n=p*q;//ceci calcule l'entier de blum
cout<<endl<<" L'entier de Blum
est:"<<n;
cout<<endl<<"Entrer la valeur pour calculer
le germe:";//Le germe,un entier premier avec n
cin>>s;
X=(s*s);
X=X%n;//calcule du germe
for(int i=1;i<=10000;i++)
{
X=(X*X)%n;//
B=X%2;//calcule les bits de la séquence
cout<<B;
}
getch ();
}
Nous savons que l'entier de Blum est défini par   , où   et   sont tous deux congrus à 3 modulo 4. En d'autres termes   et   . Nous prenons   et  petits, avec   et   .
Alors   et   , alors   ,prenons   , puisque   ,la séquence comportera 10.000 bits.
La séquence était produite en 1,20 secondes dans
un ordinateur dont les caractéristiques sont :
Ø Dual Core , Processeur AMD Sempron (tm) 2.10 GHz
Ø 3.00 Go de RAM
Voici la sequence :
011100001010110011000110100111000001011000001000000101010101110101101111110111110100011110100100100011000100100010010010000001111100010111010101111110100001010101101011101100001111111001101100100000110111000000101010011101010101111100100010111110111111101010111111001110100101111010000001101110001101100010111101000100110000010000101001110110110101000011010011100000001111110110100110110101010100100110100111011010100101001001111011001111010001000101000111110100011000110110000110010110001000000101101010111001110101010001100100110111100110110111011101101000100110011000011100101001000101011010010011011101000001100001111111010000001010101001000110100010111101000100111001010101011010001100011101011111010000011000110101111011001010001110111100101101101111101110110100101000011001111010000011110100001000111100000010011111111100010111011111100010001001001110010111010101001111000101010011001010000111010000000011011010110101011000111100011111100100110110000010101100101111000111000111111110100001110100000101110100011110001001011100100001111001101100101100001101011100010111011000001011100000101010111000100111001010100110101111011111001111001101000000000101111111101000000001001110011010010011011110110110011111100001001010000111000111000110100111001010100011111100011010100111110001110010011000101001110101111111100011110001111001010001011011000001110001111110000010011011001000011101000001110001101101010010010000011101111111101100101100110000000011100011110100101101010010010000100010110010010101010101011000110100100111111111010001010101000011001010111100111111000011000001110011010011111011000111100000101101011010011000010000000111011100011100110011011011010001100101001011010001011101110111101100100010100000001100111011111000100011000100110000110001110010000000011000101100000100110100101010101011010011001011010111111100011001011011011110000110101111101011111000000000101000000100011100100000111110010100111010110101101011011000010001001111011100100010001010010000000010010010000001001111011010101101011111000001111110000010100011101011011110011011000111011011111100011011001000101001001010110011010011110101111101011111010110111101011011110011100011001100101010011010010111100101100111010001000100000011100100110010001111000010010010100110001001100000110010100011010001101000010111000100100001000010001000001010111010110001100010001101100000001010011100101000011011000001011001001011011111000100101010010011111101101110010110100010110101111101100111010010101111110110111011111100110100010011111010010011010010000011110000001110000011100000010011010000101000101110001001001101100000000001001110110100110001000101100011000110010000100100010001001000101100110001010010100111011100010001110100111100011101100001011110100001110100001100000110010011110001100000010000000111000001001000111010001011101010110000010011010000100010101001001100111011100010011011010000100001001110111111000100011100111010011000000110000101001111111101111100001010111000100000101111000111101010011000110111010010100110101010110110001010011001101000001101001100111101101110001101011111101011100100000101101101010010111001110011001111110011110000110111000100111010100001111111101110011000110110000101110111101000001110100100010101101110101011101100101001111100110100100011100110111001010011010110010100111100010010011010111000111101010110011100010101111101011111111111101101010100011010000000110101101101001100000010111001101100010100100001001110001000101000001100110010010011011000000011011000100001100110111110111111111000100101100000011001111110110110110110011010111001000010100100110000111100101011100111011001100110000110000111000101100111000100010111011101001110110101011001111010101111001000101000110111000011000111110111100011000010010101101100001111100100111001100110101000001011010000000010110101000111011110111011001101001011010110111111000000001110000011110001110011010101100101001000001111100011111101010000010101101001010100100101110011001000111101111100011100010011100001011001101001101100100111110111001011111001001011011111010111000100011000110000100000000100000110001110011010111001111101101000001101111000100101111000111010001110000001111101110100011100101101010010010000000110010101110011001011101010011000010101000100001111101001110111010010010000011011100000001110000001110110010101000101010101001001001011001111001111001011110000001100010010110001100111101110011000111001000010011000111111010100110101101101001101111000001100100010110110110001010010010101101100101100000000101001000001111110001110001101100000100101110000101001001010111110000110110101000111111011110010000101011111010110100110101011011110100101110110001100100100000000010011001100000110011111011010000001111011101001100111001010000100001000000000011101101001011110011100000010000011001001010111111010011100000010010111101110001111110011010011010000001000111100000100010001101111011100110011000010011001010011001000011001010101110110010001100001011000010011100101101111111110011010000101010000111001100000111110101011011011001000101011011001010100110101110110100001111111
001111101111001001111111001110110011110101001010010100111010010100111110011001100000001000010010101000111000111111100000110100111001010110101101110111110110111110111001010101011101011010101101010011000000010011000101100110011010111110110011011000111111011000110000111111100110100111010110011100111100001001111010000100101000111010111000101100110000100000111010001000010100000000000111000110101011100011110000111100111010001001100001110100001011111010010100011011111000110011010110001110101000011100000101011110011001100010000011110010101011001111011100110011001001100000110000101110101001110110010111101011100011011001001010010111010111100110000011101100010010010010111111011011101111111110101111110100000010110110100111111001111001001111000110111111100101011111111111010001000100011100101011100000001101111101100001001001010001101110010101001110100111001110110101001111110011101111101110111010110001000101001010101100001111101101100000001110010000000000000001011100001010011101110110001100101101111011101110111101101001110100010010111110101101110011001011000000001011011101100100101011010111111111100001101000100010110110000000011010000110010011000111010011010000111110001000100110111010110000111011001101010111001010001110001111000100100001110110011101111101010000000010000001110000100010001111001000101110111111010110011010101100000101101111111010010100000011010100100101000001010110100111100000100010010000111001011001111010110111010110101011011010111011000101011011000000101111110011001101111010100110010101001000101101101001101000000000110101011111001101110101101000101111010100010000001110100100111110111010110110101010111101000111101010101100100110011010000011111000011011100100111001111111001101000110111010100110011110100100001010111100111100001101010010000001010011010010110011000010100000001111000101100111010000000000001000011111000100001111001111001010011110001001000010101000000001011101010110111100110001100010011110111001111100000111100100100010100010001111100100001100011100111011011101011001010010101101001001011100111000110011000011010011101101110111000011000000010000110001100110100111010001011111100000011001000110111110001110010010101111011111010111110101010111111100111001100100000010010011000011111000000010011100000101111010111111110000001010010110011110111110110101101001000111011011000110010011110110101110011010011100111000000011110000001010001101001001010000001111110000010111100110000011100111011001111101010011111110011110101110010010001001111110011000100001010010101101111110010010111100011011100001001110011000110001001010111011100100110110110001110001001000000100101111110101111000011000001111100100001110111001111010111110010101100101011110101111010000011011000001000111101011000101100100001011000001100011110010101010111000101001000111010000100011000010001101110001010111001111101011010101010000000000101100100010110011000100100000000101011001111001100100000010101000001010010101100000111111000001001010000000000010111100100001010110101100101100101101100001011101001011101110001110110000000010101101101101110000010101011100001000100001100110010101011100101111011111001101110111001011101111000001101011110110001101100010110001111110111010101110011101011111101101101111000001000111011000011011010011110101110100100001101100110001110000011101000011010010111001001101100110110011011010101100000110001111010110001110111011110011100110000111000110000011010011110100101100101111010001101111100111111111100110111111110001010001111101110010101100110101001111101001111010110011110001001010100101101110100111010001100001110111001011010010100111101110001011010000110101010000001010010011001010111010111111110110010101011000101000000101101010100001010010111101000110111000010000001010010110101010000101001101011100010010011100111000011110010001110101100001101001111111100011011000010111011001101010110010101011110010011101101001000101110100001000100010001011101001100101010001110011000011001101010101010110011010111000110001101011011100000111100111001100010111001011101011001100111011000011000001111001100000110000011101001010000010110010110000000101111000101100010111000010111110100000100001010100010111001110001001010011101010100100011011010110110001000100111111111110011000111001100011010011100111111010011011001101011101111010011011010011001100010000001111100110110111111000100001010110011100111011111110101110000101000111011010101011000001100010010110000111011100010110101010100101111110001111101110100011010111011010001110010011011111101010011011011100111101011100000001010100110111010110001011101110101011000100101110111100011010000110000111110110010111111000011111010101111100001110111011110010011100010100101101101011001101001110001101111110110001100001010100100011000111110110010011100110101111011100110011010010011111011110100101101010100011010000100100011011001110011101000011010000100111010101111000000100010011100100110001101100111010111010011001100101011110111010010101101011111101001010110000101100000100101111011000000
La séquence binaire aléatoire produite peut
être utilisée pour clés au chiffrement par flot ou au
chiffrement de verman enfin de répondre aux conditions du
théorème de Claude Shannon sur la sécurité parfaite
: une nouvelle clé est tirée à chaque chiffrement, la
clé est aussi longue que le texte clair, toutes les clés sont
équiprobables.
Si nous avons un message   de   bits à chiffrer, on considère les   premiers bits de la séquence aléatoire
générée qui constituent un mot   et on fait l'opération « ou exclusif bit à
bit » entre le message et la partie de la séquence
aléatoire considérée comme clé. C'est-à-dire
 
Il est à noter que l'expéditeur et le
destinateur ont le même générateur. A la réception,
le destinateur extrait de la même façon les   premiers bits de la séquence aléatoire et calcule ensuite
  . Les deux interlocuteurs jettent la partie   utilisée et peuvent effectuer une nouvelle transaction en
procédant de même avec le reste de la clé.
Voici le schéma illustrant l'utilisation de la
séquence binaire générée avec un message quelconque
binaire  
Fig.4. Schéma illustrant l'utilisation de la
séquence binaire produite
Clé
Partie utilisée K
Nouvelle clé
Message clair  
Message chiffré  
1
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
0
.
.
.
.
1
1
1
0
0
0
0
1
0
.
1
1
1
1
0
0
0
1
0
1
1
| 
