II.3.4. Système
cryptographique parfaitement sûr
Un système cryptographique parfaitement sûr si on
a :
  En d'autres termes : la probabilité que le texte clair soit En d'autres termes : la probabilité que le texte clair soit
  sachant que le texte chiffré est sachant que le texte chiffré est   est égale à la probabilité que le texte clair soit est égale à la probabilité que le texte clair soit
  Dans ce cas le texte chiffré n'apporte aucune information sur le
texte clair. Dans ce cas le texte chiffré n'apporte aucune information sur le
texte clair.
Lemme 1
Un système cryptographique vérifiant la
propriété de sécurité parfaite et tel que   alors : alors : 
Démonstration
Fixons   tel que tel que   , on a : , on a :
  , d'après le théorème de Bayes : , d'après le théorème de Bayes :
  donc donc   ceci signifie qu'il exite au moins une clé ceci signifie qu'il exite au moins une clé   telle que telle que   . .
Par suite   , comme , comme   est injective on a : est injective on a : 
Théorème
Un système cryptographique vérifiant   ainsi que ainsi que  
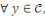  il est à la sécurité parfaite si et seulement si
les deux conditions suivantes sont réalisées : il est à la sécurité parfaite si et seulement si
les deux conditions suivantes sont réalisées :
a. Toutes les clés sont équiprobables,
b. Pour chaque   et chaque et chaque   existe une unique clé existe une unique clé   vérifiant vérifiant   . .
Démonstration
Supposons les conditions vérifiées. Alors  , on a successivement : , on a successivement :

=   , ,
=  
D'autre part pour 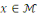  et et   , puisqu'il n'y a qu'une clé , puisqu'il n'y a qu'une clé  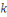 qui vérifie qui vérifie   on a : on a :

En appliquant le théorème de Bayes :

  La sécurité est donc parfaite. La sécurité est donc parfaite.
Réciproquement, supposons que la sécurité
est parfaite. Comme dans le lemme précédent, on montre que pour
chaque couple   , il existe une clé , il existe une clé   telle que telle que  . .
Pour   fixé on a donc fixé on a donc   ce qui montre que pour ce qui montre que pour   fixé l'ensemble des fixé l'ensemble des   est de cardinal est de cardinal  . Ces . Ces   sont donc distincts deux à deux et pour chaque sont donc distincts deux à deux et pour chaque   la clé la clé   vérifiant vérifiant   est unique. est unique.
Pour deux clés   et et   , comparons , comparons  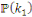 et et   . Pour cela fixons . Pour cela fixons   et désignons et désignons   et et   les uniques éléments de les uniques éléments de   vérifiant vérifiant   et et   (chaque (chaque   est injective et donc ici bijective. est injective et donc ici bijective.
Par le théorème de Bayes, et à la
sécurité parfaite on obtient :

Le même calcul peut être fait avec   Ce qui prouve que Ce qui prouve que   Les clés sont donc équiprobables. Les clés sont donc équiprobables.
Exemple
Le chiffrement de Verman ou le one-time-pad ou encore le
masque jetable vérifie les conditions du théorème
précédent. C'est un système parfaitement sûr. Il
utilise une clé secrète très longue (séquence
aléatoire binaire) où chaque bit est indépendant des
autres et une probabilité   d'être d'être   ou ou   . Une nouvelle clé est utilisée à chaque
chiffrement, la clé est aussi longue que le texte clair. La construction
de cette clé aussi longue sera l'objet de notre chapitre suivant. . Une nouvelle clé est utilisée à chaque
chiffrement, la clé est aussi longue que le texte clair. La construction
de cette clé aussi longue sera l'objet de notre chapitre suivant.
[4], [6], [7], [8], [9], [10], [11], [14] , [17],
[19],[20], [21], [22], [23], [24],[25], [26],
[27]
| 


