II.3. Sécurité
d'un système cryptographique
On distingue deux approches fondamentales dans l'étude
de la sécurité d'un cryptosystème : la
sécurité parfaite de Shannon et la sécurité
calculatoire.
II.3.1. Notions
élémentaires de probabilité
Définition classique de
probabilité
Considérons une expérience aléatoire   possédant la symétrie mutuelle et possédant la symétrie mutuelle et   un événement quelconque relatif à un événement quelconque relatif à   La probabilité de l'événement La probabilité de l'événement   est le nombre est le nombre   , où , où   est le nombre de cas favorables à est le nombre de cas favorables à   et et   le nombre total des éventualités rattaché à
l'épreuve. le nombre total des éventualités rattaché à
l'épreuve.
Définition axiomatique de
probabilité
Une mesure de   définie sur un espace probabilisable définie sur un espace probabilisable   , l'application , l'application   qui vérifie les 3 axiomes suivants : qui vérifie les 3 axiomes suivants :
 1. 1. 
2. Si   pour pour  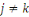
alors  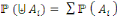 ; ;
 3. 3. 
Le triplet   est appelé espace probabilisé. est appelé espace probabilisé.
Probabilité conditionnelle
Soient   et et   deux événement telque deux événement telque  
On appelle probabilité conditionnelle de
l'événement   par rapport à l'événement par rapport à l'événement   , ou encore la probabilité de A étant donné
B : , ou encore la probabilité de A étant donné
B :

La probabilité conditionnelle nous permet de calculer
la probabilité de l'intersection :

Indépendance stochastique des
événements
Deux événements   et et   sont indépendant si sont indépendant si

si   et et   et que les événement et que les événement   et et   sont indépendants alors sont indépendants alors 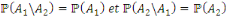 
Les événements   sont indépendants si sont indépendants si

Théorème de Bayes
Si   est un système complet d'événements et est un système complet d'événements et   est un événement quelconque. est un événement quelconque.
Supposons que   puisse se produire qu'en combinaison avec l'un des
événements de puisse se produire qu'en combinaison avec l'un des
événements de   , c'est-à-dire , c'est-à-dire   . .
  , alors on a la formule de Bayes , alors on a la formule de Bayes

Preuve. Voir [12]
II.3.2. La
sécurité calculatoire
La sécurité calculatoire est basée sur la
mesure de la quantité de calcul nécessaire pour casser un
système. On dit qu'un procédé est sûr au sens de la
théorie de la complexité si le meilleur algorithme pour le casser
nécessite   opérations où opérations où   est un nombre beaucoup trop grand pour que cet algorithme soit
applicable en pratique. Dans la pratique, on dit souvent qu'un système
est sûr si la meilleure attaque connue ne peut se faire avec une
quantité raisonnable de temps de calcul. Le problème de cette
approche c'est qu'un cryptosystème peut être sûr pendant un
moment puis ne plus l'être lorsque l'on découvre un algorithme
plus efficace. est un nombre beaucoup trop grand pour que cet algorithme soit
applicable en pratique. Dans la pratique, on dit souvent qu'un système
est sûr si la meilleure attaque connue ne peut se faire avec une
quantité raisonnable de temps de calcul. Le problème de cette
approche c'est qu'un cryptosystème peut être sûr pendant un
moment puis ne plus l'être lorsque l'on découvre un algorithme
plus efficace.
II.3.3 La
sécurité parfaite de Shannon
Claude Shannon en 1949 dans son article
intitulé « Communication Theory of Secrecy
System » introduit la notion des systèmes cryptographiquement
sûrs, qui eut une influence considérable sur l'étude de la
cryptographie.
Considérons l'ensemble fini   de textes clairs, l'ensemble fini de textes clairs, l'ensemble fini   de textes chiffrés, l'ensemble fini de textes chiffrés, l'ensemble fini   de clés. de clés.
Supposons qu'une clé   est utilisée une et une seule fois. est utilisée une et une seule fois.
Notons que l'ensemble des textes clairs   est muni d'une probabilité est muni d'une probabilité   ainsi que l'ensemble des clés ainsi que l'ensemble des clés   muni d'une probabilité muni d'une probabilité  
Supposons que les clés sont choisies
indépendamment des textes clairs.
Ainsi les deux probabilités   et et 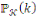  induisent une probabilité sur l'ensemble des textes
chiffrés induisent une probabilité sur l'ensemble des textes
chiffrés   Nous pouvons calculer la probabilité Nous pouvons calculer la probabilité   que le texte chiffré que le texte chiffré   soit transmis. soit transmis.
Pour une clé     , notons que , notons que   représente l'ensemble des textes chiffrés avec la
clé représente l'ensemble des textes chiffrés avec la
clé 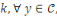  nous définissons nous définissons
  , qui est l'ensemble de toutes les clés possibles qui permettent
d'obtenir le chiffré , qui est l'ensemble de toutes les clés possibles qui permettent
d'obtenir le chiffré  
Nous avons alors la probabilité de   donnée par : donnée par :

L'événement « le texte chiffré
est   » n'est possible que si » n'est possible que si   ou ou   . .
La probabilité d'avoir le « texte
chiffré   » est la somme de toutes les probabilités mutuelles » est la somme de toutes les probabilités mutuelles
  les événements « le texte clair est les événements « le texte clair est   » et « la clé est » et « la clé est   » sont supposés indépendants, alors cette
probabilité est égale à » sont supposés indépendants, alors cette
probabilité est égale à   . .
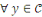  et et   ,nous pouvons calculer la probabilité conditionnelle ,nous pouvons calculer la probabilité conditionnelle   (la probabilité que (la probabilité que  soit le texte chiffré en sachant que soit le texte chiffré en sachant que   est la texte clair) par est la texte clair) par   où où   . .
En utilisant le théorème de Bayes, nous
avons :

| 


