3.6.2. Le test de Khi-carré
Le test de Chi Carré est un test qui fonctionne sur
le tableau d'effectifs à double et qui permet de contrôler, soit
l'homogénéité de sous populations par rapport à une
variable discrète, soit l'indépendance de deux variables
discrètes. La ou les variables sont quelconques, quantitatives ou
qualitatives, mais le nombre de classes doit être fini (ou rendu fini par
groupement).
Il n'y a pas d'autre différence entre le test
d'homogénéité et le test d'indépendance que la
présentation de la situation concrète sur laquelle porte le test.
Dans la présentation entre le test
d'indépendance et le test d'homogénéité, on
considère 2 variables définies sur une même population, on
dispose d'un tableau croisé (cfr Tableau n°......) d'effectifs (ou
tableau de contingence) et on teste l'indépendance des variables X et
Y.
Considérons 2 variables A et B tels que la variable
A a un certain nombre d'observations k et la variable B un certain nombre
d'observations b et  des fréquences observées respectivement me niveau pour A
et je me niveau pour la variable B, pour i=1,2, ...k et j=1,2, ...b. Le
tableau n0.... donne le format définissant les 2 variables des fréquences observées respectivement me niveau pour A
et je me niveau pour la variable B, pour i=1,2, ...k et j=1,2, ...b. Le
tableau n0.... donne le format définissant les 2 variables
Tableau n°......
|
1
|
2
|
......
|
J
|
.....
|
B
|
Total
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
....
|
|
|
|
|
|
|
|
|
i
|
|
|
|
|
|
|
|
|
...
|
|
|
|
|
|
|
|
|
a
|
|
|
|
|
|
|
|
|
Total
|
|
|
|
|
|
|
|
 est le nombre total des observations dans la ieme ligne est le nombre total des observations dans la ieme ligne
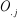 est le nombre total des observations dans la je me colonne est le nombre total des observations dans la je me colonne
Définissons  comme étant la probabilité pour la ligne i, i=1,2 ....a
et comme étant la probabilité pour la ligne i, i=1,2 ....a
et  comme étant la probabilité pour la colonne j, j=1,2,
....b comme étant la probabilité pour la colonne j, j=1,2,
....b
Le test exige que l'on puisse d'abord déterminer les
fréquences attendues 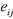 et que l'on veille à ce que les et que l'on veille à ce que les  soient supérieure ou égale à 5 ( soient supérieure ou égale à 5 (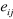 = 5). Le calcul des fréquences attendues pour la ligne i et la
colonne j utilise la formule suivante : = 5). Le calcul des fréquences attendues pour la ligne i et la
colonne j utilise la formule suivante :
 Pour i=1,2,......a et j=1,2,....b. Pour i=1,2,......a et j=1,2,....b.
Le test est formulé de la manière
suivante :
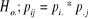 (Variables A et B sont indépendantes) (Variables A et B sont indépendantes)
 (Variables A et B sont dépendantes) (Variables A et B sont dépendantes)
Pour i=1,2,......a et j=1,2,....b.
La détermination de degré de liberté
permet de fixer laquelle de formule faudra t-il prendre en considération
entre les 2 formules ci-après :
Le degré de liberté 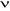 se calcule se calcule 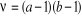 pour le seuil de signification á ou a=nombre de lignes et b =
nombre de colonnes dans le tableau pour le seuil de signification á ou a=nombre de lignes et b =
nombre de colonnes dans le tableau
 si si  >1 et >1 et  si si  =1 =1
Pour prendre la décision de rejet de Ho on
procède de 2 façons : usage des tables et de logiciel
SPSS
· usage des tables : dans ce contexte on compare la
valeur de Khi-carré calculé (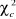 ) et Khi carré tabulé ( ) et Khi carré tabulé ( ). Si ). Si  > > on rejette Ho ceci indique que les 2variables sont
dépendantes et si on rejette Ho ceci indique que les 2variables sont
dépendantes et si  > > on accepte Ho ceci indique 2 variables sont
indépendantes on accepte Ho ceci indique 2 variables sont
indépendantes
· Usage SPSS : dans ce contexte on rejette
Ho si p-value (p) < á et on accepte Ho si p-value (p)
> á
4. Conclusion
A travers le logiciel SPSS, nous avons
directement la valeur de Pearson, le dl et le value. Ce qui nous permet de
rejeter Ho si value (P) <alpha (a) et on retient dans le cas contraire. Par
exemple considérons que a=0.05 et p=0.034 alors p=0.034<0.05 dans ce
cas on rejette Ho
En dehors des tableaux de fréquences, des pourcentages
et reste de Chi carre, nous avons fait aussi recours aux techniques d'interview
auprès des clients et auprès des consommateurs de la Compagnie de
Valorisation Industrielle de la Banane au Rwanda (COVIBAR SARL) ainsi
qu'à la technique documentaire en vue de compléter nos
résultats.
| 


