5.8.2.2 Variation du nombre de camions
Pour différentes valeurs du nombre de camions (Nbrc),
on simule 5 réplications pour un nombre de chauffeurs variant entre Nbrc
et deux fois Nbrc avec un horizon de 10000 unitéde temps et on obtient
les résultats suivant :
|
Nombre de
camions
|
R'eplications
|
Moyenne
|
Nombre de
camions
|
R'eplications
|
Moyenne
|
|
1 2 3 4 5
|
1 2 3 4 5
|
|
1
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
4
|
4
|
4
|
4
|
4
|
4
|
|
3
|
6
|
6
|
6
|
6
|
6
|
6
|
4
|
8
|
8
|
8
|
8
|
8
|
8
|
|
5
|
9
|
9
|
9
|
9
|
9
|
9
|
6
|
11
|
11
|
11
|
11
|
11
|
11
|
|
7
|
13
|
13
|
12
|
13
|
12
|
12.6
|
8
|
14
|
14
|
14
|
14
|
14
|
14
|
|
9
|
16
|
16
|
16
|
15
|
16
|
15.8
|
10
|
17
|
17
|
17
|
17
|
17
|
17
|
|
11
|
19
|
19
|
19
|
19
|
18
|
18.8
|
12
|
20
|
20
|
20
|
20
|
21
|
20.2
|
|
13
|
22
|
22
|
22
|
22
|
22
|
22
|
14
|
23
|
23
|
23
|
23
|
23
|
23
|
|
15
|
25
|
25
|
25
|
25
|
25
|
25
|
16
|
27
|
27
|
27
|
27
|
26
|
26.8
|
|
17
|
27
|
28
|
28
|
28
|
27
|
27.6
|
18
|
29
|
30
|
29
|
29
|
30
|
29.4
|
|
19
|
31
|
31
|
31
|
31
|
30
|
30.8
|
20
|
32
|
32
|
32
|
32
|
32
|
32
|
|
21
|
33
|
33
|
34
|
34
|
33
|
33.4
|
22
|
35
|
35
|
35
|
35
|
35
|
35
|
|
23
|
36
|
37
|
37
|
37
|
37
|
36.8
|
24
|
39
|
38
|
38
|
38
|
38
|
38.2
|
|
25
|
40
|
40
|
40
|
40
|
40
|
40
|
26
|
41
|
42
|
41
|
41
|
41
|
41.2
|
|
27
|
43
|
42
|
43
|
43
|
42
|
42.6
|
28
|
44
|
44
|
45
|
44
|
45
|
44.4
|
|
29
|
46
|
45
|
46
|
46
|
45
|
45.6
|
30
|
47
|
48
|
47
|
47
|
47
|
47.2
|
|
31
|
48
|
48
|
49
|
49
|
48
|
48.4
|
32
|
50
|
50
|
50
|
50
|
50
|
50
|
|
33
|
52
|
51
|
52
|
52
|
52
|
51.8
|
34
|
53
|
53
|
52
|
53
|
54
|
53
|
|
35
|
54
|
54
|
54
|
55
|
55
|
54.4
|
36
|
56
|
56
|
55
|
56
|
55
|
55.6
|
|
37
|
57
|
58
|
57
|
57
|
57
|
57.2
|
38
|
59
|
58
|
60
|
58
|
59
|
58.8
|
|
39
|
60
|
60
|
61
|
60
|
60
|
60.2
|
40
|
61
|
62
|
63
|
62
|
62
|
62
|
|
41
|
62
|
63
|
63
|
63
|
62
|
62.6
|
42
|
64
|
65
|
65
|
64
|
65
|
64.6
|
|
43
|
65
|
66
|
66
|
66
|
66
|
65.8
|
44
|
67
|
68
|
67
|
68
|
67
|
67.4
|
|
45
|
71
|
68
|
69
|
69
|
70
|
69.4
|
46
|
69
|
72
|
70
|
70
|
70
|
70.2
|
|
47
|
72
|
72
|
72
|
71
|
73
|
72
|
48
|
73
|
74
|
73
|
74
|
73
|
73.4
|
|
49
|
74
|
74
|
73
|
75
|
75
|
74.2
|
50
|
77
|
76
|
77
|
75
|
75
|
76
|
|
51
|
78
|
76
|
78
|
78
|
78
|
77.6
|
52
|
77
|
80
|
78
|
80
|
79
|
78.8
|
|
53
|
80
|
81
|
82
|
79
|
83
|
81
|
54
|
80
|
82
|
84
|
81
|
82
|
81.8
|
|
55
|
87
|
83
|
84
|
84
|
83
|
84.2
|
56
|
83
|
85
|
86
|
86
|
85
|
85
|
|
57
|
86
|
89
|
84
|
86
|
85
|
86
|
58
|
87
|
85
|
88
|
88
|
87
|
87
|
|
59
|
88
|
88
|
90
|
92
|
87
|
89
|
60
|
88
|
92
|
93
|
89
|
88
|
90
|
|
61
|
91
|
90
|
88
|
93
|
92
|
90.8
|
62
|
91
|
90
|
90
|
93
|
91
|
91
|
|
63
|
91
|
93
|
93
|
91
|
98
|
93.2
|
64
|
96
|
95
|
96
|
99
|
95
|
96.2
|
|
65
|
92
|
95
|
93
|
94
|
98
|
94.4
|
66
|
99
|
96
|
95
|
99
|
95
|
96.8
|
|
67
|
97
|
95
|
96
|
98
|
97
|
96.6
|
68
|
93
|
98
|
96
|
96
|
95
|
95.6
|
|
69
|
99
|
98
|
96
|
102
|
99
|
98.8
|
70
|
96
|
98
|
95
|
104
|
98
|
98.2
|
|
71
|
100
|
101
|
99
|
97
|
97
|
98.8
|
72
|
101
|
97
|
100
|
101
|
100
|
99.8
|
|
73
|
105
|
105
|
97
|
99
|
105
|
102.2
|
74
|
106
|
102
|
102
|
101
|
101
|
102.4
|
|
75
|
104
|
103
|
106
|
100
|
103
|
103.2
|
76
|
102
|
101
|
104
|
105
|
103
|
103
|
|
77
|
107
|
101
|
104
|
101
|
105
|
103.6
|
78
|
101
|
104
|
102
|
100
|
102
|
101.8
|
|
79
|
102
|
103
|
107
|
104
|
106
|
104.4
|
80
|
102
|
104
|
106
|
104
|
106
|
104.4
|
|
81
|
103
|
104
|
97
|
102
|
106
|
102.4
|
82
|
106
|
101
|
102
|
102
|
100
|
102.2
|
|
83
|
100
|
104
|
102
|
105
|
103
|
102.8
|
84
|
106
|
105
|
108
|
109
|
103
|
106.2
|
|
85
|
101
|
103
|
107
|
102
|
104
|
103.4
|
86
|
104
|
104
|
102
|
102
|
103
|
103
|
|
87
|
102
|
102
|
105
|
104
|
106
|
103.8
|
88
|
101
|
103
|
107
|
99
|
102
|
102.4
|
|
89
|
106
|
104
|
102
|
107
|
102
|
104.2
|
90
|
100
|
104
|
102
|
102
|
106
|
102.8
|
|
91
|
102
|
101
|
102
|
103
|
108
|
103.2
|
92
|
103
|
102
|
101
|
102
|
104
|
102.4
|
|
93
|
108
|
100
|
103
|
106
|
106
|
104.6
|
94
|
108
|
102
|
100
|
103
|
100
|
102.6
|
|
95
|
103
|
104
|
100
|
103
|
105
|
103
|
96
|
102
|
103
|
102
|
105
|
102
|
102.8
|
TAB. 5.12 - Nombre de chauffeurs correspondant au nombre de
camions par la simulation
Du tableau ci-dessus, on remarque que le nombre de chauffeurs
augmente linéairement en fonction du nombre de camions, mais
après une certaine limite, on constate qu'il a tendance a` se stabiliser
comme le montre la figure suivante :
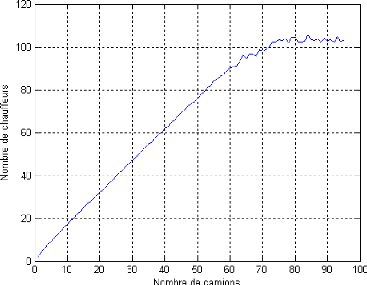
FIG. 5.9 - Nombre de chauffeurs en fonction du nombre de
camions.
Pour trancher sur la valeur du nombre de chauffeurs Nbrch,
correspondant a` un nombre précis de camions a` prendre, on va effectuer
un ajustement par un modèle de régression, puis tester sa
validité.
On remarque que l'allure du graphe n'est pas linéaire,
par conséquent il faudra chercher un modèle de régression
correspondant. En effet, on a proposéplusieurs modèles de
régression qui ont la même allure que le graphe (voir annexe C) et
a` l'aide du logiciel de statistique »R», on a effectuéune
régression non linéaire sur les résultats obtenus et on a
choisit celui qui correspond le mieux.
L'équation du modèle choisit s'écrit comme
suit :
a
Y = + bruit
1 + ce-bx
C'est un modèle qui représente une croissance
sinuso·ýdale symétrique et a` l'aide du logiciel R on a
estiméses paramètres et on a obtenu les résultats suivants
:
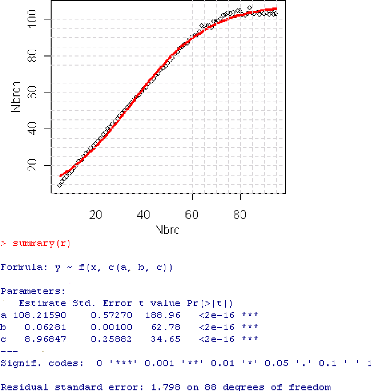
FIG. 5.10 - Ajustement par une croissance
sinuso·ýdale.
Comme on l'a mentionnéprécédemment,
jusqu'àune certaine limite du nombre de camions, le graphe a une
tendance linéaire, alors il vaut mieux de diviser nos données en
deux ensembles puis ajuster le premier avec un modèle linéaire et
le deuxième avec avec le modèle précédent.
Pour le premier ensemble (Nbrc < 60), on effectue une
régression linéaire et on obtient les résultats suivants
:
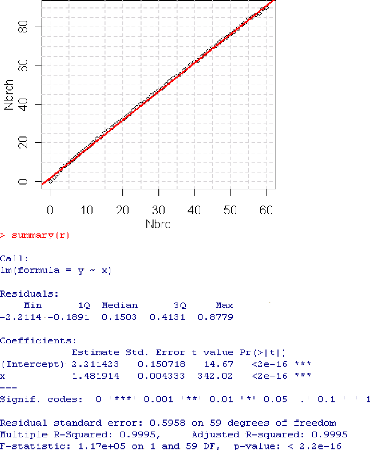
FIG. 5.11 Ajustement par une droite.
L'équation de régression linéaire
s'écrit alors sous la forme :
y= aà + àbx = 2.21 + 1.48x
Tests sur les paramètres
ta = 2.21
0.15 = 14.73.
Au niveau de á = 0.05, sur la table de Student t(n_2; '
2 ) = t(59;0.025) = 1.67.
ta = 14.73 > t(59;0.025) = 1.67. Par consequent, on
rejette l'hypothèse »a = 0».
tb = 1.48
0.0043 = 34.41.
Au niveau de á = 0.05, sur la table de Student t(n_2;'
2 ) = t(59;0.025) = 1.67. tb = 34.41 < t(59;0.025) = 1.67.
Par consequent, on rejette l'hypothèse »b =
0».
Tests sur la validation du modèle
Pour valider le modèle on teste H0 »a = b = 0»
contre H1 »a =6 0 ou b =6 0» F = 1.17 10+5. Au niveau
á = 0.05, sur la table de Ficher, f(1,59,0.05) = 4.0
F = 1.17 10+5 > 4.0. Par consequent on valide ce
modèle de regression.
Pour le deuxième ensemble (Nbrc = 60), on effectue une
regression non lineaire et on obtient les resultats suivants :
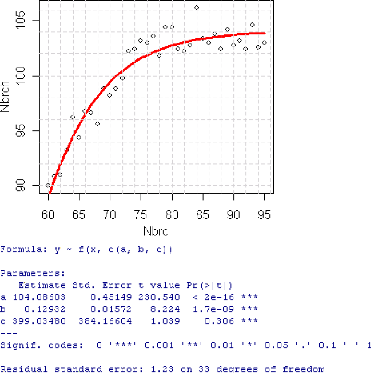
FIG. 5.12 - Ajustement par une croissance
sinuso·ýdale.
L'équation de régression non linéaire
s'écrit alors sous la forme :
aà
y= 1 + àce_àbx =
Validation du modèle
104.08
1 + 399.03.e_0.129x
Pour la validation du modèle, on utilisera la
méthode graphique en montrant que les résidus suivent bien un
processus Bruit Blanc3
A` l'aide du logiciel STATISTICA, on effectue un ajustement des
résidus et on obtient les résultats suivants :
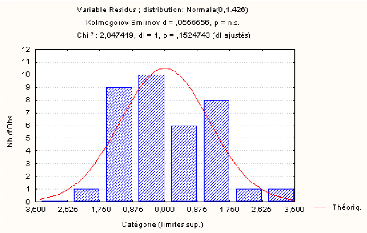
FIG. 5.13 - Ajustement des résidus par une loi
normale.
|
Test x2
|
Test Kolmogorov-Smirnov
|
|
Valeur ddl
|
Valeur
|
|
Valeur calculée
|
2.047 5
|
0.055
|
|
Valeur tabulée
|
11.07 5
|
0.216
|
TAB. 5.13 - Tests d'ajustement des résidus
On constate que pour á = 0.05 la valeur calculée
est largement inférieur a` la valeur tabulée pour les deux tests
: l'ajustement est accepté, donc on peut affirmer que les résidus
suivent bien une loi Normale de moyenne u = 0 et de variance
ó2 = 1.42.
3Bruit Blanc: suite de variables aléatoires
indépendantes de même loi, de même moyenne 0 et de
même variance ó2 finie.
De ce fait, on peut affirmer que les résidus forment un
processus Bruit Blanc et par conséquent on valide notre
modèle.
Pour déterminer le nombre de chauffeurs, correspondant a`
un nombre de camions précis, que devra avoir l'entreprise on utilisera
les modelés de régression définis
précédemment.
Pour Nbrc < 60 :
En ce qui concerne les dix premières valeurs on prendra
celles données par le simulateur car elle sont plus
représentatives puis on utilise le modèle de régression
linéaire et on obtient le tableau suivant :
|
Nombre de
camions
|
Nombre de
chauffeurs
|
Nombre de
camions
|
Nombre de
chauffeurs
|
Nombre de
camions
|
Nombre de
chauffeurs
|
|
0
|
0
|
20
|
32
|
40
|
62
|
|
1
|
2
|
21
|
34
|
41
|
63
|
|
2
|
4
|
22
|
35
|
42
|
65
|
|
3
|
6
|
23
|
37
|
43
|
66
|
|
4
|
8
|
24
|
38
|
44
|
68
|
|
5
|
9
|
25
|
40
|
45
|
69
|
|
6
|
11
|
26
|
41
|
46
|
71
|
|
7
|
13
|
27
|
43
|
47
|
72
|
|
8
|
14
|
28
|
44
|
48
|
74
|
|
9
|
16
|
29
|
46
|
49
|
75
|
|
10
|
17
|
30
|
47
|
50
|
77
|
|
11
|
19
|
31
|
49
|
51
|
78
|
|
12
|
20
|
32
|
50
|
52
|
80
|
|
13
|
22
|
33
|
52
|
53
|
81
|
|
14
|
23
|
34
|
53
|
54
|
83
|
|
15
|
25
|
35
|
55
|
55
|
84
|
|
16
|
26
|
36
|
56
|
56
|
86
|
|
17
|
28
|
37
|
58
|
57
|
87
|
|
18
|
29
|
38
|
59
|
58
|
89
|
|
19
|
31
|
39
|
61
|
59
|
90
|
TAB. 5.14 Nombre de chauffeurs correspondant au nombre de
camions par la régression
Pour Nbrc = 60 :
Pour déterminer le nombre de chauffeurs correspondant, on
utilise le modèle de régression non linéaire et on obtient
le tableau suivant :
|
Nombre de
camions
|
Nombre de
chauffeurs
|
Nombre de
camions
|
Nombre de
chauffeurs
|
|
60
|
90
|
78
|
103
|
|
61
|
91
|
79
|
103
|
|
62
|
92
|
80
|
103
|
|
63
|
94
|
81
|
103
|
|
64
|
95
|
82
|
104
|
|
65
|
96
|
83
|
104
|
|
66
|
97
|
84
|
104
|
|
67
|
98
|
85
|
104
|
|
68
|
99
|
86
|
104
|
|
69
|
99
|
87
|
104
|
|
70
|
100
|
88
|
104
|
|
71
|
100
|
89
|
104
|
|
72
|
101
|
90
|
104
|
|
73
|
101
|
91
|
104
|
|
74
|
102
|
92
|
104
|
|
75
|
102
|
93
|
104
|
|
76
|
102
|
94
|
104
|
|
77
|
103
|
95
|
104
|
TAB. 5.15 - Nombre de chauffeurs correspondant au nombre de
camions par la régression
Remarque 5.3. Le nombre maximum de chauffeurs, d'après le
modèle de régression non linéaire, que devra avoir
l'entreprise est :
~
lim
x--+8 1 + 399.03.e_0.129x
104.08 ) = 104.08 105
| 


