5.8.2 Mod`ele sans file
Contrairement au mod`ele pr'ec`edent, ce mod`ele n'a pas de
condition d'ergodicit'e (il existe toujours un r'egime stationnaire), par
cons'equent on peut simuler pour un nombre de camions Nbrc > 1.
On fixe le nombre de camions a` 75 et avec un horizon de 10000
jours, on ex'ecute notre simulateur avec un nombre de chauffeurs allant de 75
a` 150 et on obtient les r'esultats suivants :
481512,7
486939,7
482591,4
462967,9
473569,5
544135,1
18,0547
45,5157
15,8912
15,0896
27,6242
15,1122
36,3875
15,2008
15,2136
10,4561
18,3571
473743
4,4539
54,521
15,27
137
110
119
128
101
83
92
463109,4
485838,8
473110,6
475816,2
477358,2
494264,2
17,3937
53,1894
18,3966
16,0149
15,1123
26,5905
15,1978
14,9613
62,6505
35,5041
478625
554091
9,6283
15,274
15,084
44,354
15,306
3,9161
127
100
109
118
136
145
82
91
TAB. 5.11 - Resultats de la simulation pour le modele sans
file
476715,7
463055,4
490438,5
486442,1
472705,1
477018,1
15,2787
34,5807
61,5027
15,0814
15,2704
18,9092
16,0526
16,3973
25,6146
52,6083
15,1999
15,1291
15,2551
569308
487572
3,6286
8,6859
43,346
117
144
108
126
135
90
99
81
584277,8
495308,8
473407,2
477997,5
480305,6
485363,2
467896,1
42,4367
60,3094
15,5698
15,1406
24,4252
15,1558
33,4523
15,0523
51,3155
16,3591
15,2371
15,1411
465832
8,0997
19,414
3,3176
15,053
107
134
116
125
143
80
89
98
594604,4
501081,4
479862,9
486537,6
483400,3
467394,5
471331,5
469896,1
32,3867
15,1424
15,0074
16,5652
15,3878
14,7538
23,4332
15,1065
15,2202
41,5302
50,6155
15,2731
2,7937
59,247
19,768
7,3669
124
106
115
133
142
97
79
88
610261,4
512815,2
471598,9
465935,3
470358,8
478385,2
477253,6
488254,6
13,8677
14,9897
15,1834
20,2948
16,9645
15,0932
31,3623
58,4868
15,4611
15,1131
22,3971
15,1901
40,5041
49,219
2,5311
6,9291
114
105
123
132
141
87
78
96
469737,7
625430,3
517552,6
480619,4
464077,3
478098,8
480981,2
487460,5
39,5104
20,8059
17,1366
15,7723
13,3043
21,3346
15,0912
30,3602
15,1289
48,4183
15,1758
57,4759
15,1991
2,2382
6,1691
15,071
104
113
122
140
131
77
86
95
640866,7
525574,6
474366,5
469332,8
484679,5
487560,2
480982,1
21,3256
15,5873
29,5269
38,6646
15,2673
56,5076
17,4152
12,0492
47,6082
15,1972
15,2601
15,2241
473258
20,589
5,5691
15,311
1,962
103
112
130
139
121
94
76
85
656542,8
539057,8
464964,4
471168,6
477024,6
484445,6
487528,4
474354,5
55,5347
21,8533
11,0796
15,1363
19,4205
28,4743
15,2006
37,5118
15,2778
46,6279
15,2143
15,1741
5,1747
1,6854
17,872
15,605
102
120
129
138
111
84
75
93
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrch
Nbrch
Nbrch
Nbrch
Nbrch
Nbrch
Nbrch
Nbrch
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Le graphe de la fonction f(Nbrch) est
représentédans la figure suivante :
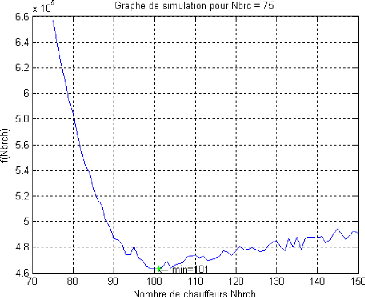
FIG. 5.8 - Graphe de la fonction perte pour Nbrc = 75.
5.8.2.1 Interprétation des résultats
Même chose que pour le mod`ele préc`edent, la
courbe a la même allure, sauf que ici le nombre de camions
inoccupés par unitéde temps correspondant a` un nombre de
chauffeurs précis est plus important et diminue faiblement a`
l'augmentation du nombre de chauffeurs, ce qui justifie l'augmentation du
besoin en chauffeurs.
Apr`es une certaine limite du nombre de chauffeurs, le nombre
de camions inoccupés par unitéde temps se stabilise autour de
15.506 qui représente le nombre de camions inoccupés par
unitéde temps (m - N) dans le syst`eme modéliséavec les
camions seuls et d`es que le nombre de chauffeurs dépasse cette limite,
la courbe a tendance a` croàýtre. Alors, cette limite
représente le nombre total de chauffeurs que doit avoir l'entreprise.
Pour cette exécution, le nombre total de chauffeurs qui
minimise la fonction perte est Nbrch=101 chauffeurs.
|
|



