5.8 Mise en oeuvre du simulateur
Pour déterminer le nombre de chauffeurs correspondant
a` un nombre de camions précis, l'idée est de faire varier le
nombre de chauffeurs partant du nombre de camions jusqu'àdeux fois ce
nombre, puis trouver un compromis entre le nombre de camions inoccupés
par unitéde temps (NbrcI) et le nombre de chauffeurs inoccupés
par unitéde temps (NbrchI).
Pour définir ce compromis, on définit une
fonction qui va lier le nombre de camions et le nombre de chauffeurs
inoccupés par unitéde temps en introduisant leurs pertes
respectives qu'ils engendrent a` l'entreprise.
Lors d'une livraison, l'entreprise considère que le
client paye un prix de transport de sa marchandise estiméa` Pc = 30000
DA par unitéde temps. Alors si un camion reste inoccupé, cette
somme est considérée comme un manque a` gagner (perte).
De plus un chauffeur est payéPch = 560 DA par
unitéde temps que se soit qu'il travaille ou qu'il reste
inoccupé, par conséquent ses jours d'inoccupation en dehors des
jours de repos sont considérés comme pertes pour l'entreprise.
La fonction perte s'écrit alors sous la forme :
f(Nbrch) = Pc * NbrcI + Pch * NbrchI -? min. 5.8.1 Modèle
avec file
On fixe le nombre de camions a` 75 et avec un horizon de 5000
jours, on exécute notre simulateur avec un nombre de chauffeurs allant
de 75 a` 150 et on obtient les résultats suivants :
466863,7
450332,9
470981,6
478053,6
463070,2
462564,5
487569,2
15,2564
15,0764
14,8884
36,0924
15,0068
18,3438
15,0882
45,3708
15,2338
0,2302
15,186
27,503
54,563
9,604
137
110
119
128
101
83
92
467950,7
480772,4
454097,2
460858,6
476310,5
474235,6
15,5974
14,9836
15,1948
26,0868
15,2136
14,9826
15,0308
53,3008
15,3866
17,5072
35,5402
465648
496752
0,0514
14,875
62,775
8,195
44,21
127
100
109
118
136
145
82
91
460646,7
460963,7
478184,7
480028,7
488208,7
489384,3
464929,6
TAB. 5.9 - Resultats de la simulation pour le modele avec file
473831,1
25,6914
52,2834
61,4264
15,2142
16,3102
15,3148
14,8622
34,0422
43,4192
15,127
0,0434
16,312
15,129
15,025
15,061
7,537
117
108
126
144
135
90
99
81
476041,7
473126,7
483809,7
510406,3
456543,9
459132,8
476341,6
463619,1
15,0994
15,0196
15,2586
24,2556
15,2414
42,2084
14,9234
15,0024
17,0132
15,0012
51,1422
0,0184
6,3606
14,983
60,246
33,571
107
134
116
125
143
80
89
98
451517,824
463219,872
532187,4
470088,5
478454,5
482469,2
486307,2
470269,1
23,5734
17,7392
14,9538
14,4462
15,2356
15,0662
15,1742
41,4796
15,1408
15,1016
59,3916
0,0204
5,1854
32,326
50,438
15,171
124
106
115
133
142
97
79
88
456767,7
457607,0
554300,8
469857,2
481931,2
487765,9
463748,1
488171,1
18,4764
49,7234
15,3696
14,9788
14,8422
22,0376
15,0768
15,3052
15,3442
58,4928
15,167
0,0158
4,7502
31,345
13,221
40,67
114
123
105
132
141
87
78
96
473902,7
464955,4
575843,2
445434,8
487772,8
470199,1
19,1944
14,8338
12,0358
15,0996
21,3704
30,3914
15,1856
57,5086
14,7922
15,0232
451754
477726
15,106
15,062
39,362
48,268
0,02
2,98
104
113
122
140
131
77
95
86
482211,7
466702,4
597532,3
457911,9
456854,9
469740,2
472728,8
481731,2
19,9174
15,2164
15,0184
15,1744
29,4004
15,0424
15,1714
11,2552
15,1092
38,3158
47,4808
15,0228
56,2996
0,0184
2,5356
20,483
103
130
139
112
121
94
76
85
476423,7
619850,4
456965,6
454440,3
461860,5
469812,3
472855,5
483900,9
15,2036
10,1684
19,2938
15,1298
28,4256
15,0646
37,3528
15,2596
55,0496
20,6612
14,9582
15,0352
46,6302
14,8532
0,0258
1,5316
102
120
129
138
111
84
93
75
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
f(Nbrch)
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrchl
Nbrch
Nbrch
Nbrch
Nbrch
Nbrch
Nbrch
Nbrch
Nbrch
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Nbrcl
Le graphe de la fonction f(Nbrch) est
représentédans la figure suivante :
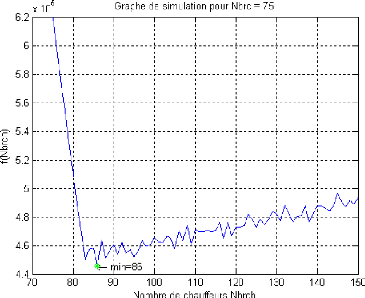
FIG. 5.4 - Graphe de la fonction perte pour Nbrc = 75.
5.8.1.1 Interprétation des résultats
On constate que lorsqu'on augmente le nombre de chauffeurs, le
nombre de camions inoccupés par unitéde temps diminue,
contrairement au nombre de chauffeurs inoccupés par unitéde temps
qui augmente, par conséquent, la courbe de f a tendance a`
décroàýtre très rapidement au début et cela
est dàu a` la perte engendrée par un camion inoccupé(30000
DA) qui est largement supérieur a` celle engendrée par
l'inoccupation d'un chauffeur (560 DA).
Après que le nombre de chauffeurs atteigne une certaine
limite, le nombre de camions
inoccupés par unitéde temps a`
tendance a` se stabiliser autour de 15,0073 qui représente
le nombre de camions inoccupés par unitéde temps
(m - ñ) dans le système modéliséavec les
camions seuls et dès que le nombre de chauffeurs dépasse cette
limite, la courbe
a tendance a` croàýtre. Alors, cette limite
représente le nombre total de chauffeurs que doit avoir l'entreprise.
Pour cette exécution, le nombre total de chauffeurs qui
minimise la fonction perte est Nbrch=86 chauffeurs.
Remarque 5.2. Lors de la simulation avec un horizon
très petit, on constate qu'il peut y avoir, sur le graphe de la fonction
perte, des pics non significatifs comme on le voit sur la figure ci-dessous qui
represente une simulation avec un horizon T=1000 unites de temps :
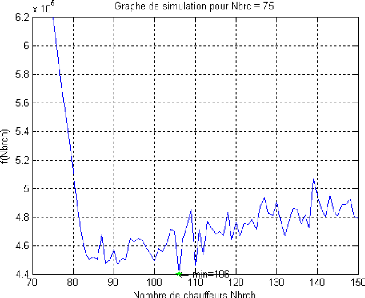
FIG. 5.5 - Graphe de la fonction perte avec des pics non
significatifs.
Pour faire face a` ce problème, on fixe l'horizon de
simulation a` 10000 (soit 27 ans), et on remarque que le graphe de la fonction
f a tendance a` se lisser comme le montre le graphe suivant :
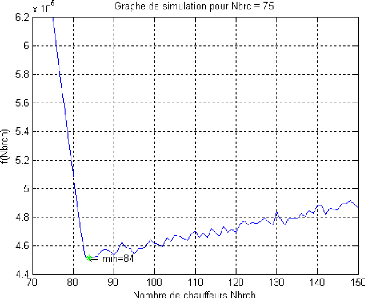
FIG. 5.6 - Graphe de la fonction perte lissé.
Dans ce qui suit, la simulation se fera avec un horizon de 10000
unités de temps. 5.8.1.2 Variation du nombre de
camions
Pour différentes valeurs du nombre de camions (Nbrc),
on simule 5 réplications pour un nombre de chauffeurs variant entre Nbrc
et deux fois Nbrc avec un horizon de 10000 unitéde temps et on obtient
les résultats suivant :
|
Nombre de
camions
|
Réplications
|
Moyenne
|
|
1
|
2
|
3
|
4
|
5
|
|
60
|
90
|
90
|
92
|
90
|
90
|
90.4
|
|
61
|
86
|
85
|
87
|
88
|
86
|
86.4
|
|
62
|
85
|
84
|
84
|
86
|
85
|
84.8
|
|
63
|
85
|
85
|
87
|
86
|
85
|
85.6
|
|
64
|
87
|
85
|
84
|
84
|
84
|
84.8
|
|
65
|
85
|
83
|
83
|
85
|
88
|
84.8
|
|
66
|
85
|
86
|
85
|
85
|
84
|
85
|
|
67
|
86
|
86
|
84
|
87
|
84
|
85.4
|
|
68
|
85
|
85
|
84
|
84
|
84
|
84.4
|
|
69
|
83
|
83
|
85
|
84
|
83
|
83.6
|
|
70
|
85
|
87
|
83
|
85
|
89
|
85.8
|
|
71
|
84
|
87
|
86
|
84
|
90
|
86.2
|
|
72
|
83
|
89
|
83
|
83
|
87
|
85
|
|
73
|
83
|
83
|
83
|
84
|
88
|
84.2
|
|
74
|
84
|
90
|
83
|
87
|
85
|
85.8
|
|
75
|
85
|
87
|
88
|
83
|
84
|
85.8
|
|
76
|
85
|
84
|
83
|
85
|
84
|
84.2
|
|
77
|
88
|
87
|
84
|
84
|
85
|
85.6
|
|
78
|
83
|
90
|
85
|
85
|
83
|
85.2
|
|
79
|
85
|
84
|
84
|
83
|
84
|
84
|
|
80
|
83
|
85
|
84
|
85
|
86
|
84.6
|
TAB. 5.10 - Nombre de chauffeurs correspondant au nombre de
camions par la simulation
Du tableau ci-dessus, on constate que la moyenne du nombre de
chauffeurs n'a pas de tendance et varie autour de 85 indépendamment du
nombre de camions comme le montre la figure ci-après, a` l'exception de
la première valeur qui est une valeur non significative car elle
représente la condition d'ergodicité, par conséquent les
caractéristiques correspondantes du système sont très
difficile a` atteindre par le simulateur.
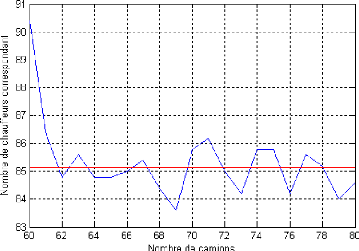
FIG. 5.7 - Ajustement du nombre de chauffeurs.
Pour trancher sur la valeur du nombre de chauffeurs Nbrch a`
prendre, on va effectuer un ajustement par une droite, puis tester la
validitédu modèle.
A` l'aide du logiciel de statistique »R», on a
effectuéune régression linéaire simple sur les moyennes
calculées et on a aboutit aux résultats suivants :

L''equation de r'egression lin'eaire s''ecrit alors sous la forme
:
y= aà + àbx = 85.32 -- 0.02737x
Tests sur les param`etres
ta = 805.3.32 2 = 266, 62.
Au niveau de á = 0.05, sur la table de Student
t(n-2; 2) = t(18;0.025) = 2.101.
ta = 266, 62 > t(18;0.025) = 2.101. Par
cons'equent, on rejette l'hypoth`ese »a = 0».
tb = |-0%02297639 7| = 0.92.
Au niveau de á = 0.05, sur la table de Student t(n-2; 2) =
t(18;0.025) = 2.101. tb = 0.92 < t(18;0.025) = 2.101.
Par cons'equent, on accepte l'hypoth`ese »b = 0» ce qui
veut dire que le nombre de chauffeurs et le nombre de camions ne sont pas li'es
et que y est une constante.
Le mod`ele sera alors y=85.32 ce qui veut dire que l'entreprise
doit avoir 86 chauffeurs ind'ependamment du nombre de camions.
|
|



