3.3 Estimation par intervalle de confiance[16]
On appelle intervalle de confiance au niveau (1 - á) pour
un param`etre è, l'intervalle [T1(x1, x2, .., xn),T2(x1, x2,
.., xn)] tel que :
P(T1(x1, x2, .., xn) = è = T2(x1, x2, ..,
xn)) = 1 - á,
avec á donne, T1(x1, x2, .., xn) et T2(x1, x2,
..,xn) sont appeles limites de confiance de è au niveau (1 -
á).
Soit èà un estimateur ponctuel de
è. Pour determiner les bornes de confiance, on doit determiner les deux
constantes î1 et î2 telles que :
á1 = P(T < è - î1) et á2 = P(T
> è + î2) ,
á1 = á2 = á2, avec
á donneet T=àè.
On a P(è - î1 < T < è + î2) = 1 -
á, par transformation on aura :
f T < è + î2 f è > T - î2
T > è - î1 lè < T +
î1
Ce qui donne P(T - î2 < è < T + î1) = 1
- á , Alors les deux statistiques sont :
ü T1(x1, x2, .., xn)=T-î2,
ü T2(x1, x2, ..,xn)=T+î1.
3.4 Loi r'egissant le besoin journalier en camions
Pour determiner le nombre moyen ainsi que le nombre minimum
et maximum de camions utilises, on a eu recours aux donnees concernant le
nombre journalier de camions utilises dans les dix mois derniers (Aoàut
jusqu'au mois de Mai), comme le montre le tableau suivant :
Date i
|
Nombre de camions utilises a` la date i
|
19/08/2006
|
48
|
.
.
|
.
.
|
24/05/2007
|
51
|
|
TAB. 3.1 - Nombre journalier de camions utilises
3.4.1 Application au cas d'Ifri
Soit X » Le nombre de camions utilises en un jour
donne»
3.4.1.1 Ajustement des données avec le test de
Khi-deux :
Soit un 234-échantillon constituédes
données concernant le nombre journalier de camions utilisés dans
les dix mois derniers (Aoàut jusqu'au mois de Mai). On veut tester si la
loi de X est une loi de poisson, donc on va tester:
H0 »Poisson est la loi de X» Contre H1 »Poisson
n'est pas la loi de X»
En partitionnant le domaine des valeurs de X en 7 classes, le
tableau suivant nous donne l'effectif empirique de chaque classe, les
probabilités théoriques rattachées, l'effectif
théorique, le pourcentage cumuléthéorique et
observé.
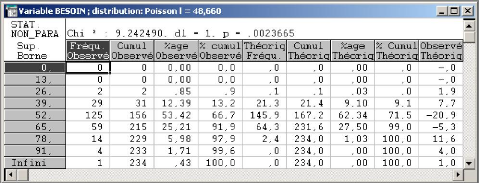
FIG. 3.1 - Tableau représentant les paramètres
calculés La réalisation de la statistique de décision nous
a donné:
K2 n
|
=
|
Xn
i=1
|
(Ni - npi)2
npi
|
= 9.24.
|
|
Dans la table de Khi-deux, on a :
÷2 (r-1-1,á) = ÷2 (5,0.05) = 11.07,
tel que r représente le nombre de classes et á le
niveau de signification.
K2 n =
|
Xn
i=1
|
(Ni - npi)2
npi
|
= 9.24 < ÷2(r-1-1,á) = ÷2
(5,0.05) = 11.07,
|
|
d'o`u on accepte que le nombre de camions utilisés a` une
date donnésuit une loi de poisson de paramètre ë=48.66.
X P(ë = 48.66).
Le schéma suivant nous montre le graphe d'ajustement par
la loi de poisson. En rouge l'histogramme de la loi de poisson, en bleu
l'histogramme des données observées.
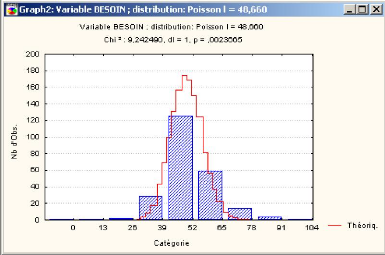
FIG. 3.2 - Graphe d'ajustement par la loi de poisson
Conclusion :
Avec les données récoltées, le test de
Khi-deux révèle que la loi régissant le besoin journalier
en camions est poissonnienne de paramètre A = 48.66.
Pour confirmer et justifier l'acceptation du processus
poissonnien comme processus qui régis le nombre de camions
utilisés, on va refaire le test d'ajustement par une loi de poisson et
cela par le test d'ajustement de Kolmogorov-Smirnov.
| 


