Soit un 234-échantillon constituédes
données concernant le nombre journalier de camions utilisés dans
les dix mois derniers (Aoàut jusqu'au mois de Mai) de fonction de
répartition F, on veut tester si la loi de X est une loi de poisson,
donc on va tester :
H0 »Poisson est la loi de X» Contre H1 »Poisson
n'est pas la loi de X»
En partitionnant le domaine des valeurs de X en 7 classes, le
tableau suivant nous donne l'effectif empirique de chaque classe, les
probabilités théoriques rattachées, l'effectif
théorique, le pourcentage cumuléthéorique et
observé.
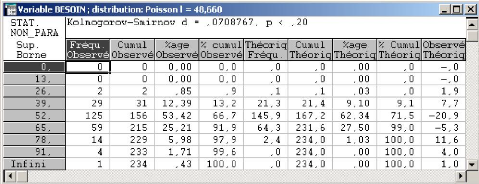
FIG. 3.3 - Tableau représentant les paramètres
calculés
Le plus grand écart entre la distribution empirique et la
distribution théorique (loi de poisson) est :
D = max |Fn(x) - F0(x)| = 0.070,
tel que F0 est la fonction de répartition de la loi de
poisson. Dans la table de Kolmogorov-Smirnov on a :
1.30
d(N, a) = d(234, 0.05) = v234 = 0.085,
avec N représente la taille de l'échantillon et a
le niveau de signification. D = max |Fn(x) - F0(x)| = 0.070 <
d(N, a) = 0.085,
d'o`u on accepte que le nombre de camions utilisés a` une
date donnésuit une loi de poisson de paramètre A estiméa`
48.66.
Le schéma suivant nous montre le graphe d'ajustement par
la loi de poisson. En rouge l'histogramme de la loi de poisson, en bleu
l'histogramme des données observées.
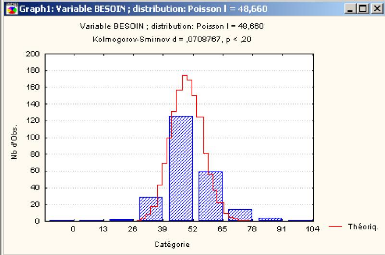
FIG. 3.4 - Graphe d'ajustement par la loi de poisson
Conclusion :
Le test de Kolmogorov-Smirnov nous confirme que le processus
r'egissant le besoin journalier en camions est poissonnien. Donc on peut
affirmer que la loi de X est une loi de poisson de paramètre A =
48.66.



