2.5 Quelques systèmes de files d'attente
2.5.1 Le système M/M/1
Une file M/M/1 compte un seul serveur offrant un service dont
la durée est une variable exponentielle de taux u indépendant de
l'état du système et recevant des clients selon un processus de
poisson de taux constant A . Il s'agit làdu plus simple parmi les
modèles de files d'attente. Il permet, cependant, d'illustrer les
principaux phénomènes observés dans ce systèmes.
Représentant l'état d'un tel système a`
un instant quelconque par le nombre de clients présents, le graphe des
transitions possible entre ses différents états correspond a` la
figure ci-dessous. Pour étudier une telle file, nous pouvons nous
rabattre directement sur la théorie des processus de naissance et de
mort. Un système M/M/1 en constitue, en effet, un cas très
particulier, chaque arrivée d'un client pouvant être
assimilée a` une naissance et chaque départ a` une mort. Le taux
d'arrivée qui correspond au taux de naissance est constant et
égal a` A. Tout comme le taux de service, correspondant au taux de mort,
qui vaut u, tout au moins tant qu'il y a des clients dans le
système[9].
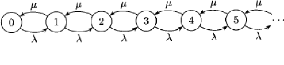
FIG 2.5
2.5.1.1 Régime transitoire
Vu les propriétés fondamentales du processus de
poisson et de la loi exponentielle, le processus (X(t))t~0 : »nombre de
clients dans le système a` l'instant t», est markovien. Les
équations différentielles de Kolmogorov de ce processus sont de
la forme :
~P 0 0(t) = --AP0(t) + uP1(t), (2.5)
P
0 n(t) = --(A + u)Pn(t) + APn--1(t)
+ uPn+1(t), m = 1, 2,
·
·
· . Ce
système d'équations permet de calculer les probabilités
d'états Pn(t) en faisant appel
aux équations de Bessel et si l'on connaàýt
les conditions initiales (X(0)).
2.5.1.2 Régime stationnaire
lim
t'--+oo
Lorsque t tend vers l'infini dans le système (2.5), on
peut montrer que les limites pn(t) = ðn existent et
sont indépendantes de l'état initial du processus et que :
|
lim
t'--+oo
|
0
pn(t) = 0, V m =
0,1,
·
·
·
|
Ainsi, a` la place d'un systeme d'equations differentielles, on
obtient un systeme d'equations {
lineaires et homogenes :
uð1 = kr0,
ëðn-1 + uðn+1 = (ë + u)ðn, n =
1, 2
·
·
· .
00
De plus, nous avons la condition E ðn = 1
car (ðn)n est une distribution de pro-
n=0
babilite.
La solution de ces equations est donn'ee par :
|
ðn = ð0 (ë
u
|
n ë
) = (1 --
u)(uë)n , n = 0, 1,
·
·
·
|
a` condition que ë < u (condition d'ergodicitegeometrique
du systeme). On montre que le regime stationnaire du systeme M/M/1 est
gouvernepar la loi geometrique.
2.5.1.3 Quelques caract'eristiques
· Le nombre de clients dans le systeme : Si on note cette
caracteristique par N, alors :
N = E(X) =
|
00
E
n=0
|
nðn = (1 -- ñ)
|
00
E
n=0
|
nñn = ñ = ë .
1 -- ñ u -- ë (2.6)
|
|
ñ= ë est la charge du systeme. u
· Le nombre de clients dans la file : Notons cette
caracteristique par Q. Soit Xq le nombre de clients se trouvant dans
la file d'attente, on a :
Xq = { 0, si X = 0
X -- 1, siX > 1.
Alors :
|
Q = E(Xq) =
|
00
E
n=1
|
ë2
(n -- 1)ðn = (2.7)
u(u -- 1).
|
|
T =N
ë
|
=
|
ñ
|
|
1/u
|
|
1
-- A' (2.8)
u
|
|
ë(1 -- ñ)
|
|
1 -- ñ
|
|
W =
Q
ë
|
=
|
ñ2
|
|
ñ
|
ñ
(2.9)
u -- ë.
|
|
ë(1 -- ñ)
|
|
u(1 -- ñ)
|
D'autres caracteristiques comme le temps moyen de sejour T et
d'attente W d'un client dans le systeme peuvent àetre calculees a`
l'aide de la formule de Little.
| 


