Planification et gestion du parc de transport au niveau de la SARL Ibrahim et fils

2.5.2 Le système M/M/m [9]

Une file M/M/m poss`ede m serveurs identiques partageant les mêmes places d'attente et servant chacun un client a` la fois. La dur'ee d'un service est une variable al'eatoire distribu'ee d'apr`es une loi exponentielle de param`etre u et les clients arrivent dans le syst`eme d'apr`es un processus de Poisson de taux ë. Comme pour le cas pr'ec`edent, le processus d'ecrivant l''evolution du nombre de clients dans le syst`eme est un processus de naissance et de mort. On peut donc d'eriver les 'equations d''equilibre a` partir de son graphe repr'esentatif (fig.2.6.)

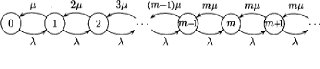
FIG 2.6

2.5.2.1 Régime stationnaire

Le syst`eme pouvant traiter m clients en parall`ele, un maximum de mu clients quittent la file par unit'e de temps. Le taux d'arriv'ee des clients 'etant de ë par unit'e de temps, l'intensit'e du trafic d'une file M/M/m est ñ = ë/mu et une telle file est stable si et

seulement si

ë

ñ = < 1 . (2.10)

mu

Sous cette condition, la r'esolution des 'equations de bilan fournit les probabilit'es stationnaires

I (mñ)k

k! ð0, k=1,. . .,m-1

ðk = (2.11)

ñ^km^m

m! ð0, k=m,m+1,...

Ainsi

^m-1X^ð0( k=0

ñk k! +

X8 k=m

m! mm ( ^ñ m)^k) = 1,

Il en r'esulte

"m-1X ñk k! + ñm ð0 = m!(1 - ^ñ m) k=0

I-1

.

(2.12)

ñk-m = ð0 m!(1 - ñ). (2.13)

æ =

X8 k=m

ðk = ð0

(mñ)^m m!

X8 k=m

(mñ)^m

Pour les syst`emes a` plusieurs serveurs, il est utile de calculer la probabilit'e æ qu'un client qui arrive doit attendre, c'est-à-dire la probabilit'e que tous les serveurs soient occup'es. Cette probabilit'e est connue sous le nom de formule C d'Erlang, est 'egale a`

2.5.2.2 Quelques caractéristiques

Utilisant les r'esultats pr'ec'edents, le calcul des performances de la file n'est pas diff'erent du cas de la file M/M/1. Le nombre moyen N de clients pr'esents dans le système et le nombre moyen Q de clients en attente sont

N= _X8

k=1

kðk = mñ + ñæ

1 - _ñ, (2.14)

Q =

X8 k=m+1

(k - m)ðk = ñæ 1 - ñ. (2.15)

Une simple application de la formule de Little permet d'obtenir les expressions des temps moyens de s'ejour T et d'attente W :

N T = ë	1 æ = + mu(1 - ñ), (2.16) u
Q W = ë		æ = mu(1 - ñ). (2.17)

Pour calculer le taux d'utilisation de chaque serveur, remarquons que, pendant un intervalle de temps suffisamment long ô, un nombre moyen de ëô clients entreront dans le système. Le traitement de ces clients demandera, en moyenne, un temps total 'egal a` ëô u . Le taux d'utilisation de chaque serveur s'obtient en r'epartissant ce temps sur les m serveurs et en divisant par le temps d'observation :

ëô/u U = mô

ë = = ñ. (2.18) mu

Théorème 2.3. (théorème de Burke[6])

Pour les systêmes M/M/m, si ë < um alors le flot des departs est poissonnien de paramêtre ë > 0.

P(ç < t) = 1 - e^-ët,

ç : duree d'intervalle entre deux departs successifs.