I.4. Equations polynomiales dans C
I.4.1. Théorème de d'Alembert
Théorème
Tout polynôme non constant (c'est - à - dire de
degré supérieur à 0) à coefficients complexes,
admet au moins une solution dans C.
Conséquence
Tout polynôme P non constant à coefficients dans
C se factorise en un produit de polynôme du
1er degré. Le nombre de racines de P est donc n, chacun
étant compté autant de fois que sa multiplicité.
Racines complexes d'un polynôme à coefficients
réels
Soit P = anxn +
an-1xn-1 + ... + a1x + a0 un
polynôme à coefficients réels. Soit  une racine non réelle de P, avec la multiplicité m. Alors une racine non réelle de P, avec la multiplicité m. Alors
 est une racine de P avec la même multiplicité. est une racine de P avec la même multiplicité.
I.4.2. Racines carrées d'un complexe non nul
Proposition
Tout nombre complexe non nul z admet exactement 2 racines
carrées, qui sont opposées. La méthode est la suivante, en
posant  et en cherchant et en cherchant  sous la forme sous la forme 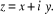
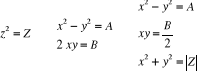
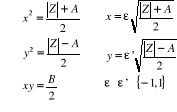
 du signe de du signe de 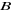
Alors 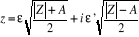
I.4.3. Racines n-ièmes d'un nombre complexe non
nul
Définition
Soit z un nombre complexe non nul, et n un entier naturel non
nul. On appelle racine n-ième de Z tout nombre complexe z tel que
zn=Z.
Proposition
Soit  la forme trigonométrique de la forme trigonométrique de  (avec (avec  ), ),  possède exactement n racines n-ièmes données
par : possède exactement n racines n-ièmes données
par :
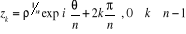
La méthode est la suivante, en cherchant z sous la
forme  . .
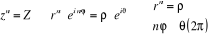
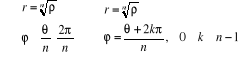
Remarques
Les points images Mk de ces n racines
n-ièmes sont les sommets d'un polygone régulier convexe inscrit
dans le cercle de centre 0 et de rayon 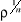
Les n racines n-ièmes  de de  apparaissent dans la factorisation apparaissent dans la factorisation 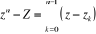
En particulier, par identification des termes de degré
n-1 et des termes constants :
· La somme des n racines n-ièmes  de de  est nulle (si n >1) est nulle (si n >1)
· Leur produit vaut 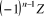
I.4.4. Racines n-ièmes de l'unité
On appelle racines n - ièmes de l'unité les
racines n - ièmes dans C du nombre 1. Elles sont
données par  avec avec  . Si on note . Si on note  alors pour tout alors pour tout  (en particulier (en particulier  ). ).
| 


