I.3.3. Forme trigonométrique
Définition
Soit  . Il existe une unique classe des réels . Il existe une unique classe des réels  définies modulo 2ð, telle que définies modulo 2ð, telle que . Cette classe de réels modulo 2ð est appelée
l'argument de z. . Cette classe de réels modulo 2ð est appelée
l'argument de z.
Chacun des réels è de cette classe est
appelé une détermination de l'argument de z (ou, par
abus de langage, un argument de z), et on note : arg z =
è (2ð).
Remarque
L'argument d'un nombre complexe non nul z possède une
unique détermination dans tout intervalle , et en particulier dans les intervalles , et en particulier dans les intervalles  et et . .
Proposition
Tout nombre complexe non nul s'écrit de manière
unique , avec , avec  et et . .  est le module de z et è est une
détermination de l'argument de z. On dit que est le module de z et è est une
détermination de l'argument de z. On dit que  est écrit sous forme trigonométrique. est écrit sous forme trigonométrique.
Remarques
 · , avec · , avec  et è réel quelconque. Parler de l'argument
de 0 n'a donc pas aucun sens. et è réel quelconque. Parler de l'argument
de 0 n'a donc pas aucun sens.
· Soit . Alors : . Alors :
 et et  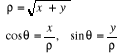
Si  (ce qui détermine è modulo ð) (ce qui détermine è modulo ð)
Si  (ce qui détermine è modulo 2ð) (ce qui détermine è modulo 2ð)
· Si  , mais si on n'est pas certain du signe du réel , mais si on n'est pas certain du signe du réel  : : 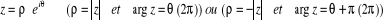
Argument et opérations dans
C
Soient u et v, no nuls :  et et   . .
 . En particulier : . En particulier : 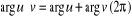
 . En particulier : . En particulier : 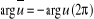
 . En particulier : . En particulier : 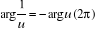
 . En particulier : . En particulier : 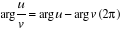
 . En particulier : . En particulier : 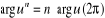
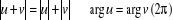
Argument et cas particuliers
Soit  un nombre complexe non nul : un nombre complexe non nul :
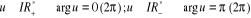
 est réel est réel 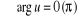
 est imaginaire pur est imaginaire pur 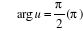
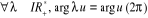
I.3.4. Fonction exponentielle complexe
Définition
Soit  (avec (avec  IR) un nombre complexe. On pose IR) un nombre complexe. On pose  , encore noté exp z. On définit ainsi une application de
C dans C, appelée exponentielle
complexe. , encore noté exp z. On définit ainsi une application de
C dans C, appelée exponentielle
complexe.
Remarques
La restriction à IR de la fonction
 est l'exponentielle réelle déjà connue. Sa
restriction aux imaginaires purs est : est l'exponentielle réelle déjà connue. Sa
restriction aux imaginaires purs est :  définie précédemment. définie précédemment.
Pour tout nombre complexe  (avec (avec  IR) : IR) :  . Ainsi . Ainsi 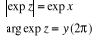
Propriétés
Pour tous nombres complexes z et z' :
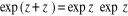
 tel que tel que  (en particulier exp 0 = 1) (en particulier exp 0 = 1)
 et et 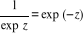
 tel que tel que 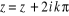
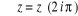
L'application exponentielle est donc périodique de
période  . .
Résolution de l'équation exp z = a
Soit  un nombre complexe non nul ( un nombre complexe non nul ( est le module de a). Pour tout nombre complexe est le module de a). Pour tout nombre complexe  (avec (avec  IR) IR)
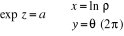 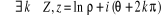
L'équation exp z = a possède donc une
infinité de solutions. Toutes se déduisent de l'une d'entre elles
par ajout d'un multiple entier de  . .
Remarques
D'après les résultats précédents,
l'application exponentielle est un morphisme surjectif du groupe
(C,+) sur le groupe (C,? ) dont le noyau est
 Z Z
L'équation exp z = a (a non nul, cherché sous
la forme  ) possède une solution unique si on se limite à ) possède une solution unique si on se limite à  (par exemple (par exemple  , ou , ou  ). ).
| 


