I. 2. Définition de C
I. 2. 1. Définition : On munit l'ensemble IR2
des deux lois suivantes :
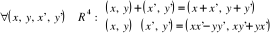
Proposition
Muni de ces deux lois, IR2
possède une structure de Corps. Plus précisément :
Le neutre pour la loi + est 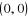
L'opposé de  est est 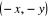
Le neutre pour la loi  (le produit) est (le produit) est 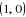
Pour tout  non nul, l'inverse de z est non nul, l'inverse de z est 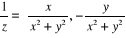
Définition : On note C
l'ensemble IR2 muni des deux lois
précédentes. Ses éléments  sont appelés nombres complexes. sont appelés nombres complexes.
Proposition :
L'ensemble  est un sous - corps de C. L'application est un sous - corps de C. L'application  est un isomorphisme de corps IR sur
IK. est un isomorphisme de corps IR sur
IK.
Conséquence
De cette manière  apparaît comme un sous - corps de apparaît comme un sous - corps de . Cet isomorphisme permet d'identifier le complexe . Cet isomorphisme permet d'identifier le complexe  avec le réel avec le réel . .
I. 2. 2. Notation cartésienne
Dans le corps , on note i = , on note i = . Pour tout . Pour tout  de C, on constate que de C, on constate que . Avec l'identification de IR avec un Sous - Corps de
C, on peut écrire . Avec l'identification de IR avec un Sous - Corps de
C, on peut écrire  . On a ainsi obtenu la notation cartésienne (ou
algébrique) des nombres complexes. . On a ainsi obtenu la notation cartésienne (ou
algébrique) des nombres complexes.
Définitions : Pour tout z de
C, il existe un couple unique  de IR2 tel que de IR2 tel que . Le réel x est appelé partie réelle de z
et est noté Re(z), le réel y est appelé partie
imaginaire de z et est noté Im(z). . Le réel x est appelé partie réelle de z
et est noté Re(z), le réel y est appelé partie
imaginaire de z et est noté Im(z).
Un nombre complexe est dit réel si Im(z) = 0,
z est dit imaginaire pur si Re(z) = 0, c'est-à-dire si z = i y,
avec y réel.
Remarques
· Soient  et et  deux nombres complexes, avec deux nombres complexes, avec . Les lois de C s'écrivent maintenant : . Les lois de C s'écrivent maintenant :
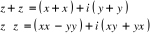
 · (On identifie les parties réelles et les parties
imaginaires) · (On identifie les parties réelles et les parties
imaginaires)
En particulier :  (attention à vérifier que x et y sont réels) (attention à vérifier que x et y sont réels)
Puissance du nombre i
On constate que i2= -1. Donc . En fait, . En fait,  . Plus généralement i3= - i
et i4= 1. Le Sous - Groupe . Plus généralement i3= - i
et i4= 1. Le Sous - Groupe  engendré par i est cyclique d'ordre 4 : engendré par i est cyclique d'ordre 4 : 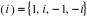
Remarque
Si  est un complexe non réel, alors on peut encore effectuer
l'identification suivante : est un complexe non réel, alors on peut encore effectuer
l'identification suivante :
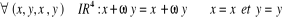
I. 2. 3. Conjugaison
Définition : Soit  (x et y réels) un nombre complexe quelconque. Le nombre complexe (x et y réels) un nombre complexe quelconque. Le nombre complexe
 est appelé le conjugué de z. On nomme
conjugaison l'application de C dans
C définie par est appelé le conjugué de z. On nomme
conjugaison l'application de C dans
C définie par . .
Proposition : La conjugaison est un automorphisme
involutif du corps (C,+,?). Cela signifie que :
· 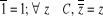
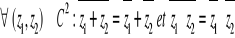
· Propriétés
· Pour tous complexes  , ,
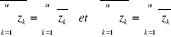
· Pour tout z complexe : 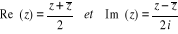
· z est réel 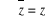
· z est imaginaire pur 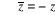
I. 2. 4. Module
Définition : Soit  un nombre complexe quelconque. On appelle module de z
la quantité notée un nombre complexe quelconque. On appelle module de z
la quantité notée  égale à égale à  . .
Remarques :
On constate que  (utile pour se « débarrasser » du module). (utile pour se « débarrasser » du module).
En particulier, si z est non nul, l'inverse de z est . .
Si z est réel, le module de z est égal à
sa valeur absolue. Les notations  (valeur absolue ou module) sont donc compatibles. (valeur absolue ou module) sont donc compatibles.
Propriétés :
L'application « module » vérifie
les propriétés suivantes :
Pour tous  de C2 : de C2 :
 · . Si z est non nul, · . Si z est non nul, 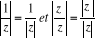
 · . Il y a égalité · . Il y a égalité 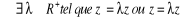
 · . Si · . Si 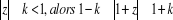
Conséquence : (C, ) est un espace normé. ) est un espace normé.
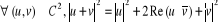
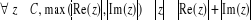
· · Généralisation :
Pour tous complexes 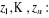
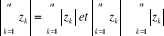
En particulier, 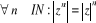
On a  les zk sont produits de l'un d'entre eux par des réels
positifs. les zk sont produits de l'un d'entre eux par des réels
positifs.
Proposition
L'ensemble U des nombres complexes de module
1 est un sous-groupe de  Pour tout z de U, Pour tout z de U, 
Proposition (Distance dans C)
Soit d l'application C x C
vers IR, définie par :
 d est une distance sur C, ce qui signifie
qu'elle vérifie les propriétés suivantes : d est une distance sur C, ce qui signifie
qu'elle vérifie les propriétés suivantes :
Pour tous nombres complexes u, v et w :
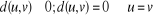
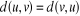
 · · · (Inégalité triangulaire) · · · (Inégalité triangulaire)
| 


