I.2.5. Fonctions à valeurs complexes
Soit X un ensemble quelconque non vide.
F(X, C) désigne
l'ensemble des applications définies sur X et à
valeurs complexes. Le plus souvent X désignera un
intervalle de IR, ou l'ensemble IN (dans ce
cas, on obtient l'ensemble des suites à valeurs complexes)
On sait que F(X,
C) est un anneau commutatif pour les lois déduites de
C, et définies par :
 F(X,C), F(X,C), 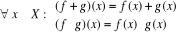
Le neutre de
F(X,C) pour la loi +
(respectivement la loi .) est l'application constante 0 (respectivement 1)
Si f appartient à
F(X, C), on définit
les éléments  de F(X, C) : de F(X, C) :
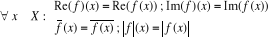
On a pour les opérations « partie
réelle », « partie imaginaire »,
« conjugaison » et « module », des
propriétés dans
F(X,C) analogues
à celles qui ont été rencontrées dans
C.
| 


