2.5. Fonctions hyperboliques
Comme pour des fonctions trigonométriques et
trigonométriques réciproques, ici aussi nous n'étudierons
que les fonctions sh et cosh (sinus hyperbolique et cosinus
hyperbolique)
2.5.1. Fonction sh
Nous voulons avoir une fonction de la forme :
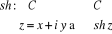
Par définition, 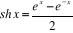
Par extension aux nombres complexes, on a :
)
1
(
sin
2
iz
i
e
e
z
sh
z
z
-
=
-
=
-

Posons 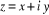
 devient devient
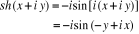
Appliquons la formule de sinus :
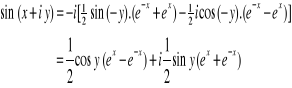
2.5.2. Fonction ch
Procédons de la même manière pour avoir
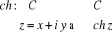
Par définition, 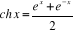
Par extension aux nombres complexes, on a :
iz
e
e
z
ch
z
z
cos
2
=
+
=
-

Posons  . On obtient . On obtient
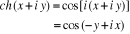
Appliquons la formule de cosinus.
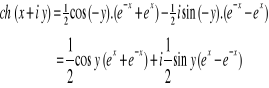
| 


