2.4. Fonctions trigonométriques
réciproques
Vu que nous n'avons étudié que deux fonctions
trigonométriques dans le paragraphe précédent, nous ne
nous limiterons ici qu'aux seules fonctions réciproques de sinus et
cosinus, c'est-à-dire les fonctions arcsin et arccos.
2.4.1. Fonction arc sinus
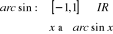
Son domaine de définition est [-1, 1]. Essayons
d'évaluer cette fonction pour n'importe quelle valeur réelle. On
obtiendrait une fonction de la forme :
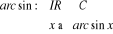
Voici comment nous pourrons procéder :
0
2
1
2
2
sin
sin
=
-
-
=
-
=
-
=
=
-
-
x
i
e
e
x
i
e
e
x
i
e
e
x
y
y
x
arc
iy
iy
iy
iy
iy
iy
Multiplions les deux membres par eiy. On a
donc :
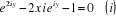
Posons eiy = z, l'équation  devient : devient :
 qui est une équation du second degré à constantes
complexes. qui est une équation du second degré à constantes
complexes.
Exemple : Calculer arc sin 2
Soit
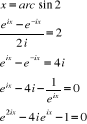
Posons eix = z
z2 - 4z - 1 = 0
3
2
12
)
1
(
)
1
(
4
)
4
(
2
i
i
=
-
=
-
-
-
=

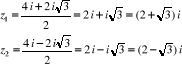
Pour  , on a : , on a :
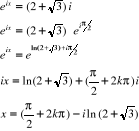
Avec 
Pour  , on a : , on a :
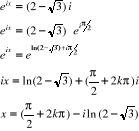
Avec 
Ainsi,
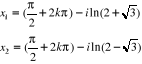
Prolongement de la fonction arc sin aux nombres
complexes
Nous voulons avoir une fonction de la forme :
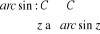
avec 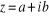
Soit  un nombre complexe, un nombre complexe,
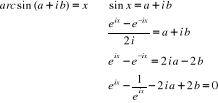
Multiplions les deux membres par 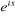
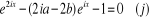
Posons  , l'équation , l'équation  devient : devient :
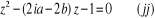
L'équation  ci - dessus est une équation du second degré à
coefficients complexes. ci - dessus est une équation du second degré à
coefficients complexes.
2.4.2. Fonction arc cos
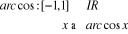
Le domaine de définition de cette fonction est [-1,
1]
Evaluation de la fonction arc cos sur toute valeur
réelle
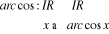
Soit  , déterminons , déterminons 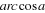
Posons  , on a , on a 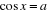
Ainsi,
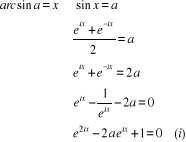
Pour  , l'équation , l'équation  devient : devient :
 qui est une équation du second degré à coefficients
réels. qui est une équation du second degré à coefficients
réels.
Exemple : Calculons arc cos 2
L'équation résolvante est 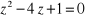
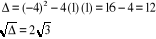
 et et 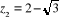
Pour  on a : on a :
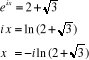
Pour  on a : on a :
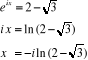
Prolongement de la fonction arc cos aux nombres
complexes
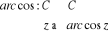
Soit  un nombre complexe, un nombre complexe,
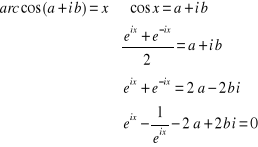
Multiplions les deux membres par 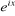
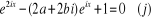
Posons  , l'équation , l'équation  devient : devient :
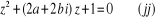
L'équation  ci - dessus est une équation du second degré à
coefficients complexes. ci - dessus est une équation du second degré à
coefficients complexes.
| 


