2.3. Fonctions trigonométriques
Parmi les fonctions trigonométriques, nous
n'étudierons que les fonctions sinus et cosinus, les autres étant
facilement déductibles à partir des deux premières.
2.3.1. Fonction sinus
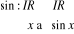
Le domaine de valeurs de la fonction sinus est [-1, 1] et son
domaine de définition est IR.
Pour étendre cette notion et exprimer les sinus des
nombres complexes on se servira de la formule :
 et et 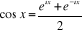
Nous voulons donc avoir les fonctions de la forme
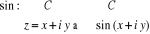
En effet,
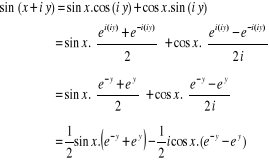
2.3.2. Fonction cosinus
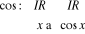
Comme la fonction sinus, la fonction cosinus est
définie pour tout réel et son domaine de valeurs est [-1, 1].
Pour la définir sur des complexes, on procède
comme suit :
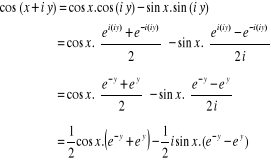
| 


