Implantation d'algorithme de filtrage numérique sur FPGA(réseau de portes programmables)

I.14. Les types de filtre numérique

Le fonctionnement de base d'un filtre numérique est relativement simple. On distingue en fait deux types de fonctionnement, illustrés sur les figures ci-dessous :

Délai

Entrée

Sortie

Figure II.4- principe d'un filtre non-récursif

On retarde légèrement une copie du signal d'entrée (d'une ou plusieurs périodes d'échantillonnage) et on combine le signal d'entrée retardé avec le nouveau signal d'entrée. Les filtres numériques basés sur ce fonctionnement sont dit à "RIF - Réponse Impulsionnelle Finie" ou FIR (pour Finite-Impulse-Response). On les qualifie également de filtres nonrécursifs.

Délai

Entrée

Sortie

Figure II.5- principe d'un filtre récursif

On retarde une copie du signal de sortie que l'on combine au nouveau signal d'entrée. Les filtres numériques basés sur ce fonctionnement sont dit à "réponse impulsionnelle infinie" ou IIR (pour Infinite Impulse Response). On les qualifie également de filtres récursifs

II.6.1 Les filtres à réponse impulsionnelle finie (RIF)

Les filtres numériques à réponse impulsionnelle finie (RIF) sont des systèmes linéaires discrets invariants dans le temps définis par une équation selon laquelle un nombre de sortie, représentant un échantillon du signal filtré, est obtenu par sommation pondérée d'un ensemble fini de nombres d'entrée, représentant les échantillons du signal a filtrer. Les coefficients de la sommation pondérée constituent la réponse impulsionnelle du filtre et un ensemble fini d'entre eux seulement prennent des valeurs non nulles. Ce filtre est du type « a mémoire finie ~, c'est-à-dire qu'il détermine sa sortie en fonction d'informations d'entrée d'ancienneté limitée. Il est fréquemment désigné par filtre non récursif, en raison de sa structure, car il ne nécessite pas de boucle de réaction dans sa réalisation, comme c'est le cas pour une autre catégorie de filtres, celle des filtres à réponse impulsionnelle infinie. [13]

II.6.2 l'équation aux différences de filtre RIF

A partir de l'équation de forme générale (l'équation II.10 ) , les coefficients b(k) sont tous égaux a zéro pour k=1 donc pour les filtres a réponse impulsionnelle finie, l'équation (II. ) vérifie :

(II.24)

La suite d'entrée et la suite de sortie sont reliées par une équation du type

suivant qui constitue la relation de définition :

(II.25)

Le filtre ainsi défini comporte un nombre N fini de coefficients ak ; considéré comme un système discret, il a pour réponse à la suite unitaire, la suite h( k ) tel que :

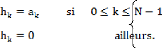
C'est-à-dire que la réponse impulsionnelle est simplement la suite des coefficients.

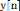
À partir de la transformée en z de l'équation (II.25), on déduit aisément la fonction de transfert du filtre, c'est-à-dire le rapport entre la transformée en z de la sortie et celle

de l'entrée
		(II.26)

Donc :

(II.27)

Elle ne présente pas de pôle mais seulement des zéros, le filtre RIF sera par conséquent toujours stable.

(II.28)

Avec :

(II.29)

L'équation représentée la réponse fréquentielle de filtre. Avec Les coefficients

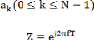
Constituent le développement en série de Fourier de cette fonction Ainsi,

pour la transformée en Z de la suite x(n) coïncide avec sa transformée de Fourier.

C'est-à-dire que l'analyse d'un filtre numérique se faire avec la transformée en Z et, pour connaître la réponse en fréquence, il suffit de remplacer Z par .