Modélisation et couverture des comptes courants postaux

12.2 Volatilité de la marge et perte en situation de stress

Nous retenons pour nos simulations le modèle à «superstrates» en situation démographique stable²⁹ à la date initiale t=0. Nous simulons alors, pour différentes valeurs du paramètre y, p=150 trajectoires de marges nettes d'intérêts jusqu'en t=h=120. Nous calculons

ensuite les valeurs prises par les statistiques A=

1000 (h - 61)L0

v u u Xh tt=62

(IRM(t) - IRM(t - 1))^2

1000

et T= (IRM(t^*))^- sur chaque trajectoire de marge nette d'intérêts simulée.

Ä0

Nous analysons alors, pour chaque y choisi, la moyenne empirique des p valeurs simulées de

A et de T, que nous noterons  (y) et T à (y).

Valeur de y	Volatilité empirique moyenne de A (c'est-à-dire Â(y)) (x10^-3)	Écart-type empirique de A (x10^-3)
1	209.6	5.3
0.7	145.8	7.2
0.5	104.2	3.4
0.3	62.9	1.3
0.1	21.5	0.7
0.05	11.4	0.6
0.07	5.6	0.6

Nous constatons que la volatilité obtenue  (y) est quasiment proportionnelle à y. La raison à ce résultat réside dans le fait que la volatilité dans la marge dégagée est essentiellement «apportée» par les fluctuations de taux d'un mois sur l'autre. Dans ces conditions, c'est le processus de tombée des flux d'intérêts, au titre des placements court-terme, qui apporte l'es-

²⁸Conformément à l'hypothèse (3) du modèle global

²⁹Sa clientèle est le reflet de la pyramide en terme de distribution d'âges

moyenne empirique

72

sentiel de la volatilité de la marge {IRM(_t)}0<t<h. Par ailleurs, la dispersion des résultats empiriques obtenus est faible, avec un écart-typeempirique qui ne dépasse jamais 5% de la Ëà (y).

( Nous avons tracé ci-dessous le graphe obtenu en reportant les points de coordonnées ) à (y) , Ë^à (y)dans le plan «perte x volatilité», afin d'illustrer l'arbitrage à effectuer entre les deux grandeurs.

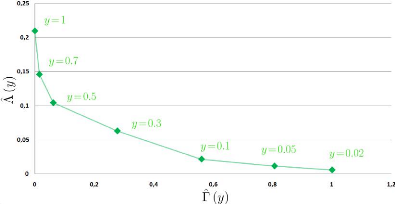
FIG. 21 - La volatilité de la marge nette d'intérêts et la perte moyenne engendrée par le scénario de stress pour différentes politiques de placement dans le cas d'une clientèle en situation démographique normale

Nous mettons bien en évidence sur cet échantillon de simulations qu'une diminution de y, c'est-à-dire une moindre proportion de l'encours placée à court terme, lisse la marge nette perçue mais accroît le risque de liquidité auquel la banque s'expose. Comme on pouvait s'y attendre, dans le cadre de ces p simulations, lorsque l'établissement place 100% de son encours total à court-terme, il s'immunise totalement contre le stress de liquidité et de taux généré : sa marge en t^* ne devient jamais négative. Dans les autres cas, suivant le scénario pour l'encours et les taux, la marge dégagée à cette même date peut être positive ou négative suivant le contexte de marché (c'est-à-dire la courbe des taux en t^*). à (y), qui fournit la moyenne empirique de la partie négative de IRM(t^*), est donc négatif pour yE{0.3,0.1,0.05,0.02}.

Il n'existe pas de stratégie «optimale», pour la simple et bonne raison que chaque banque a une définition individuelle du caractère optimal, fonction de la politique de risque à laquelle elle souscrit. Toutefois, il est légitime de se demander quelle influence la structure initiale de la base de clientèle peut avoir sur le processus de marge nette en termes de volatilité et de perte. Cette influence peut en effet conditionner le choix de la stratégie à adopter pour l'établissement. La section qui suit explore cette question.

73