Il s'agit ici d'estimer, dans le cadre de notre
modèle, la durée de vie théorique de l'encours des CCP,
sous l'hypothèse que la banque ne commercialise plus de produits. Dans
ce contexte, seuls les comptes des clients à l'heure actuelle continuent
d'évoluer dans le futur, mais aucun nouveau compte ne sera ouvert.
L'agrégat de dépôts s'éteindra donc
définitivement lorsque tous les clients actuels auront quitté
l'établissement par décision volontaire ou par
décès.
Notre modèle étant fondé sur des taux de
sortie, la décroissance de l'encours est exponentielle.
La durée caractéristique de décroissance
dépend directement de ces taux de sortie.
Voici par exemple ce que l'on obtient avec l = 2
dans les cas respectifs d'une situation démographique initiale
stable, déséquilibrée vers le haut et
déséquilibrée vers le bas. Afin de pouvoir les
comparer, les trajectoires obtenues sont renormalisées afin de
coïncider à l'origine.
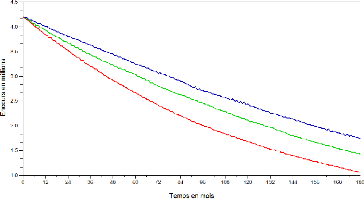
FIG. 12 - Une trajectoire avec une situation initiale
stable (courbe verte), un déséquilibre
démographique vers le haut (courbe rouge) et un
déséquilibre démographique vers le bas (courbe
bleue) de la dynamique de l'encours total avec un encours moyen par cellule
déterministe
On retrouve visuellement la décroissance exponentielle
annoncée. Remarquons toutefois que la banque s'en sort d'autant mieux
qu'elle a une population jeune à l'instant où toute
commercialisation de produits est arrêtée, ce qui est très
intuitif. Elle profite en effet du vieillissement de ses clients actuels et de
la croissance de leur richesse. A l'inverse, une banque ayant une
clientèle d'un âge avancé perd plus rapidement son
agrégat de dépôts en raison du départ rapide de ses
clients patrimoniaux.
Avec notre modèle, il faut attendre, même dans
le cas l = 2 d'une grande mobilité des clients, des
durées typiques de l'ordre de 60 ans pour épuiser totalement le
stock. En d'autres termes, certains clients actuels d'âge resteront dans
l'établissement jusqu'à avoir atteint l'âge maximum. En
réalité, il faut bien sûr tenir compte de
phénomènes que notre modèle ne
49
prend pas en compte ici, typiquement l'effet de
réputation. Il est en effet légitime de penser qu'une banque
arrêtant de commercialiser des produits ait de plus en plus de
difficultés à retenir ses clients au fur et à mesure de
son «déclin». Notre modèle peut donc être
utilisé pour simuler des trajectoires de mort de l'encours sur le
court-moyen terme (au plus quelques années). Pour des durées
importantes de plus de 10 ans, il est raisonnable de penser que le
modèle construit n'est plus valide et qu'il faut intégrer
d'autres aspects. Par exemple, cela pourrait raisonnablement s'envisager avec
des taux de sortie croissants avec le temps.



