8 Un modèle à
«superstrates»
Au vu de cette première analyse, il ressort que les
valeurs typiques que nous avons adoptées pour l
présentent toutes deux des avantages et des
inconvénients.
Ainsi, dans le cas l = 60, on constate par
comparaison avec la courbe d'évolution de l'encours des CCP sur les
quinze dernières années, que cette valeur de paramètre
fournit des courbes trop peu volatiles, comme si notre pouvoir explicatif sur
l'encours était trop élevé. En revanche, dans le cas de
déséquilibres démographiques, il permet de rendre compte
d'un effet mémoire sur le moyen-long terme qui paraît
satisfaisant.
A contrario, le paramètre l = 2 semble donner
des résultats plus conformes à la réalité sous
l'angle de la forme générale d'évolution, dans la mesure
où il permet des «sauts» plus marqués qui sont
nettement visibles sur la courbe historique. Cependant, nous avons vu que cette
valeur de paramètre entraîne des réajustements
démographiques que l'on a envie de qualifier de «trop» rapides
: ainsi, tout déséquilibre démographique interne à
la banque se résorbe en moyenne approximativement en un an, ce qui
semble a priori peu plausible. En outre, le cas l = 2
correspond à un changement de strate tous les deux mois en moyenne. Une
telle valeur de paramètre peut donc paraître artificielle, dans la
mesure où la ventilation en strates est censée capturer la
situation financière générale du client, que l'on ne
s'attend évidemment pas à voir changer aussi
fréquemment.
Le but de cette section est de proposer une forme
d'amélioration de ce que nous avons considéré jusqu'ici,
qui puisse concilier, dans la mesure du possible, les faits stylisés
évoqués ci-dessus, tout en offrant une représentation plus
crédible de la réalité.
Notre point de départ est le suivant : il est
légitime de penser que l'encours d'un client (peu importe sa situation
financière) puisse connaître de fortes fluctuations d'un mois sur
l'autre, suite à des dépenses inhabituelles ou encore à
des virements vers des supports d'épargne par exemple. Nous envisageons
donc ici une amélioration dans la calibration du modèle en
ventilant chaque strate en deux sous-strates. Ces dernières regroupent
respectivement les clients de la strate considérée dont le compte
est dans un état «haut» (fortement alimenté) et ceux
dont le compte est dans un état «bas» (peu alimenté).
Les clients ont alors une propension marquée à rester dans leur
strate, mais une forte mobilité au sein de celle-ci entre les
différentes sous-strates qui la composent. Cela correspond bien à
l'idée selon laquelle la surface financière du client est une
donnée relativement stable, tandis que l'état de son compte peut,
quant à lui, être beaucoup plus volatile! De cette manière,
on conserve un pouvoir explicatif sur l'encours du client sur le moyen-long
terme (donné par la strate à laquelle il appartient) tout en
introduisant des fluctuations «locales» mensuelles données par
les mouvements internes à chaque strate entre les deux états. Une
telle approche prend tout son sens si l'on pense à des périodes
annuelles précises, comme les fêtes de fin d'année,
où l'on peut observer des débits importants sur la
majorité des comptes courants.
50
Nous allons à présent expliciter cette
démarche. Considérons une banque de détail comprenant E =
s = 8 strates. L'idée est de les voir groupées par paire
(en tant qu'état «haut» et état «bas») au
sein de quatre «superstrates» qui représentent la surface
financière. La superstrate 1 correspond aux clients les plus
aisés et regroupe les strates i = 1 et i = 2 qui sont
respectivement ses états «haut» et «bas». La
superstrate 4 correspond, quant à elle, aux clients les plus modestes et
se compose des strates i = 7 («haut») et i = 8
(«bas»). L'état complémentaire de la strate i
au sein d'une «superstrate» sera appelé strate
binôme. Les âges des clients sont toujours compris entre
c=18 ans (et 0 mois) et w=80 ans (et 0 mois). Chacune des
5960 cellules est supposée contenir initialement n = 5 clients
: on a réparti les clients de chacune des 2980 cellules
précédentes uniformément entre les deux cellules-filles
correspondant aux états «haut» et «bas».
Les cellules de clientèle regroupant les clients les
plus âgés sont toujours caractérisées par un taux de
sortie de 1 :
Vi E E, Vk E E,
ë(i,ù) k = 0 et
o(i,ù) = 1
Soit désormais j =6 w. Nous
considérons que le taux de maintien dans chacune des (quatre)
l - 1
«superstrates» est de l ,
où l ~2 caractérise la stabilité de la surface
financière des clients.
Nous pourrons prendre typiquement l=60,
correspondant à une sortie au terme de cinq ans (en moyenne) de la
superstrate. Les sorties par décès sont par ailleurs toujours
calibrées sur
celui de passage dans l'une des (s - 2) autres strates
est pris uniforme égal à 1
les taux de mortalité publiés par l'INED. Le
taux de sortie volontaire est pris égal à 1 2l et
2l(s - 2).
En particulier, nous supposons que les clients changeant de
«superstrate» ont autant de chances de se retrouver dans les
états «haut» et «bas» de la «superstrate»
d'arrivée. En revanche, si le taux de maintien dans chaque
«superstrate» est élevé, nous souhaitons autoriser des
mouvements fréquents entre les deux strates qui la composent : pour
spécifier ce mouvement potentiel, nous introduisons un nouveau
paramètre uE[0, 1], qui mesure la propension à
rester dans le même état («haut» ou «bas»).
Plus précisément, le taux de transition vers
l'autre strate de la «superstrate» à laquelle
le client appartient est (1 - u)l - 1
l et celui de
l - 1
maintien dans sa strate actuelle est ul . En
faisant varier le paramètre u, on contrôle la
dynamique de transition d'un état à un autre au
sein d'une «superstrate». Pour u = 0.5, les deux
états sont équiprobables; pour u faible, on assure une
forme d'attirance vers la strate binôme et pour u
élevé, on assure une plus grande stabilité du client
au sein de son état actuel. Ainsi, un u proche de zéro
correspond à une situation dans laquelle la présence du client
dans un état («haut» ou «bas») au sein de sa
«superstrate» entraîne une plus forte probabilité de le
retrouver dans l'état binôme à la date suivante.
Intuitivement, si l'on adopte un tel u, on postule implicitement que,
si le client est dans son état «bas» à une date
t, alors il y a de fortes chances pour qu'il alimente son compte et
qu'il passe dans l'état «haut» en t+1.
Réciproquement, s'il est dans l'état «haut» en
t, il est probable qu'il fasse un virement de ce compte vers un livret
d'épargne et donc qu'il passe dans l'état «bas» en
t + 1. À l'inverse, pour u proche de un, on postule
simplement qu'il est plus probable que chaque client reste dans son
état.
51
Sous l'hypothèse d'indépendance entre la
mortalité et les strates vers lesquelles les personnes seraient
amenées à évoluer à la date suivante sans
mortalité, nous avons donc pour
(i, j) E E x (FL - {ù}), et en notant
i0 la strate binôme de i,
?
?????????
?????????
ë(i,j) k= 1 - ?j
si k E (E - {i, i0}) 2l(s
- 2)
ë(i,j) i=u(l -
1) (1 - ?j) si k = i
l
ë(i,j)
i0=(1 - u)(l - 1) (1 -
?j) si k = i0
o(i,j) =?j + 1 - ?j
2l
l
Enfin, les entrées sont dans un premier temps
calibrées de manière à équilibrer les sorties. En
effet, nous voulons d'abord assurer une constance démographique moyenne
dans la sous-population des clients de la banque.
V (i, j, t) E Ex(FL -
{á})xN*, é(i,j) t
Poisson (no(i,j-1)) Poisson (n
1?j-1 +
|
~~
1 - ?j-1
2l
|
|
L'encours moyen par client correspondant à la cellule
la plus modeste de la banque est normalisé, pris égal à 1.
Il s'agit des jeunes de 18 ans dans l'état «bas» de la
«superstrate» 4, autrement dit des jeunes de 18 ans de la strate
i = 8. Nous ferons ensuite l'hypothèse que l'état
«haut» correspond à un encours moyen deux fois plus
élevé que l'état «bas», et que l'état
«bas» est repris de l'encours moyen que nous avions supposé
lorsque s était égal à 4. Voici donc la matrice
Do. Nous avons fait figurer en vert les strates
correspondant à des états «hauts» et en bleu celles
correspondant aux états «bas».
Superstrate
|
Strate
|
j = á = 216
|
j = 217
|
...
|
j = 228
|
j = 229
|
...
|
j = 959
|
j = ù = 960
|
1
|
i = 1
|
8
|
8
|
...
|
16
|
16
|
...
|
496
|
504
|
|
4
|
4
|
...
|
8
|
8
|
...
|
248
|
252
|
2
|
i = 3
|
6
|
6
|
...
|
10
|
10
|
...
|
250
|
254
|
|
3
|
3
|
...
|
5
|
5
|
...
|
125
|
127
|
3
|
i = 5
|
4
|
4
|
...
|
6
|
6
|
...
|
126
|
128
|
|
2
|
2
|
...
|
3
|
3
|
...
|
63
|
64
|
4
|
i = 7
|
2
|
2
|
...
|
3
|
3
|
...
|
63
|
64
|
|
1
|
1
|
...
|
1,5
|
1,5
|
...
|
31,5
|
32
|
|
On obtient alors des formes générales
d'évolution similaires à celles que nous avons déjà
analysées, avec des variations locales d'encours assez nettes. La
différence est que ces variations sont ici principalement dues aux
mouvements des clients au sein de leur «superstrate» respective entre
les états «hauts» et «bas».
Pour discerner ces cas, nous avons simulé des
trajectoires de l'encours global de la banque pour différentes valeurs
de u. Afin de saisir l'influence de ce paramètre seul, nous
avons par ailleurs adopté une inflation constante
ð=0.002. Nous avons pris uE{0.5,
0.1} correspondant à différents cas décrits
dans le paragraphe précédent et nous avons simulé des
trajectoires de l'encours sur 10 ans.
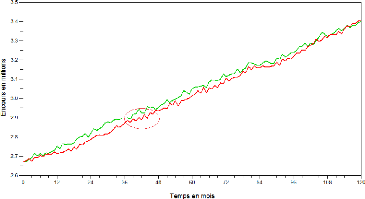
52
FIG. 13 - Une trajectoire pour
u=0.5 (courbe verte) et u=0.1 (courbe
rouge) de la dynamique de l'encours total avec un encours moyen par cellule
déterministe
Nous avons alors calculé, dans le cas u =
0.5, la volatilité renormalisée moyenne de l'encours
obtenue sur 1000 trajectoires. La volatilité correspondante s'est ainsi
avérée être seulement 3% inférieure à celle
obtenue dans le cas des strates «simples» (s=4) pour l
=2! Nous sommes donc effectivement parvenus à obtenir des sursauts
locaux de l'encours, similaires à ceux dans le modèle simple
à 4 strates pour l = 2, et ce en dépit de la valeur
l = 60! Ainsi, nous conservons ici un pouvoir explicatif fort sur
chaque client, qui a une forte probabilité de rester au sein de sa
«superstrate». Toutefois, grâce à la modélisation
simple du caractère aléatoire de l'encours personnel de chacun
d'entre eux d'un mois sur l'autre, nous créons une volatilité
locale qui diminue notre pouvoir prévisionnel sur l'encours global. Par
ailleurs, les deux trajectoires simulées ci-dessus permettent
d'entrevoir les différences de dynamique imposées par le
changement de valeur de u.
Pour u=0.1, on discerne ainsi des formes
d'alternances fréquentes entre croissance locale et décroissance
locale de l'encours d'un mois sur l'autre. Cet effet
«balançoire» est dû à l'attirance pour la strate
binôme: une situation de déséquilibre en t (plus
de personnes dans l'état «haut» que dans l'état
«bas») est suivie avec une très forte probabilité d'un
déséquilibre inverse en t + 1. C'est cet effet que nous
discernons dans les crêtes de la courbe d'évolution de l'encours.
Nous avons entouré une telle évolution caractéristique en
«dents de scie» (voir Figure 13 ci-dessus).
Toutefois, la formidable stabilité
démographique que nous imposons ici (uniformité initiale et
constance en moyenne dans le temps) ne permet pas de distinction encore
très nette des types d'évolution de l'encours futur. Nous allons
donc à présent réintroduire l'aspect
démographique.
53
Les paramètres adoptés sont l =60 et
u=0.5, correspondant à un changement de
«super-strate» tous les 5 ans en moyenne et une
équiprobabilité entre les deux états «haut» et
«bas». Les entrées sont à nouveau calibrées
conformément aux projections futures de la pyramide des âges. Nous
prenons désormais n=10.
Nous avons fait figurer sur les graphes ci-après les
évolutions respectives de l'encours avec une situation initiale
stable de la base de clientèle puis avec les deux types de
déséquilibre (vers le bas et vers le haut). Sur
chaque graphe, nous avons également fait figurer en noir la courbe
d'évolution de l'encours si celui-ci suit exactement le niveau
d'inflation (qui croît de 2.4% par an) : cela fournit ainsi une
base de comparaison pour les croissances des trajectoires simulées. En
outre, toutes les trajectoires ont été renormalisées de
manière à partir d'une origine commune, le but étant de
discerner les formes d'évolution à partir d'un même point
de départ actuel.

FIG. 14 - Une trajectoire avec une situation initiale
stable (courbe verte) et un déséquilibre
démographique vers le haut (courbe rouge) de la dynamique de
l'encours total avec une inflation constante dans le modèle à
«superstrates»
On retrouve le fait qu'un déséquilibre vers
le haut entraîne une sous-performance par rapport à
l'inflation. Dans une première phase, l'encours décroît
faiblement en raison de la perte des clients âgés qui
détiennent le plus d'encours. La tendance s'inverse cependant
progressivement en quelques années. Cela est dû à
l'inflation d'une part, mais aussi à l'augmentation du nombre de jeunes
clients, au vieillissement de la base de clientèle d'un âge
intermédiaire en t = 0 ainsi qu'à l'arrivée de la
génération du baby-boom, qui fournit un nombre croissant
d'entrées de clients d'un âge avancé. Lorsque la banque
possède initialement une base de clients stable,
c'est-à-dire calquée sur la pyramide des âges, elle
surperforme l'inflation comme nous l'avons déjà constaté
dans les modèles à strates. Cela est essentiellement lié
au vieillissement de ses clients appartenant à la
génération du baby-boom.

54
FIG. 15 - Une trajectoire avec une situation initiale
stable (courbe verte) et un déséquilibre
démographique vers le bas (courbe bleue) de la dynamique de
l'encours total avec une inflation constante dans le modèle à
«superstrates»
Dans le cas d'un déséquilibre
démographique initial vers le bas caractéristique des
banques en ligne, la surperformance par rapport à l'inflation est
très nette. Elle provient essentiellement de la croissance du nombre de
clients et au vieillissement de la clientèle existante. On obtient dans
les deux cas un rééquilibrage progressif en plusieurs
années, sans pour autant «tuer» toute volatilité locale
comme cela était le cas avec l = 60 dans le modèle
à strates simples.
Enfin, ce raffinement à «superstrates»
permet également d'intégrer l'influence de
déséquilibres de la démographie initiale de la base de
clientèle entre les états «haut» et «bas»,
afin de mieux anticiper l'évolution de l'encours sur le court terme.
Imaginons, à titre d'exemple, que l'on sache que u a une valeur
faible. Autrement dit, l'attirance pour la strate binôme est forte : un
compte bien alimenté a de fortes chances d'avoir beaucoup diminué
au mois suivant (par virement vers les comptes d'épargne par exemple).
Dès lors, si la distribution de clients présente un
déséquilibre envers un état, on obtient une forme de
rémanence locale de ce déséquilibre sur le court terme,
avec un effet oscillant qui s'amortit sur plusieurs mois. Inversement, si u
est fort, on s'attend à conserver ce biais vers les strates
«hautes» sur les mois à venir.
Pour illustrer notre propos, nous avons simulé une
trajectoire d'encours sur un an avec l= 60 et u=0.1.
Nous avons créé un déséquilibre initial en partant
de la situation démographique stable puis en
transférant, pour chaque âge j et chaque
«superstrate», un client de l'état «bas» vers
l'état «haut». Sachant que n = 10, cela
représente 10% de l'effectif de chaque cellule jusqu'à 65 ans.

55
FIG. 16 - Une trajectoire avec
déséquilibre démographique initial vers les strates
«hautes»
On observe très clairement la rémanence
annoncée, avec un effet balançoire qui s'amortit dans ce cas-ci
sur une durée typique d'une année. Au-delà, le
déséquilibre s'est effacé suite aux mouvements et
arrivées de nouveaux clients. Cela permet d'une certaine manière
de créer un mouvement de «masse» à court terme. Tout se
passe ainsi comme si l'on créait artificiellement une corrélation
entre les mouvements de clients dans le modèle à strates simples.
On obtient dès lors une liberté de modélisation
supplémentaire dont on ne disposait pas avant.
En conséquence, ce modèle peut être utile
pour affiner la prévision à court terme de
l'encours si l'on dispose de la distribution actuelle de la base des clients et
si l'on a calibré (sur la base d'observations historiques) la valeur de
u.
Finalement, ce modèle à
«superstrates», qui nous donne la possibilité de
«pianoter» sur les états «haut» et «bas»,
sur les probabilités de transition de l'un vers l'autre et sur les taux
de transition de «superstrate» nous permet de générer,
dans le cadre de valeurs de paramètres
«réalistes»16, des trajectoires de
l'encours qui respectent certains faits stylisés que nous posons a
priori :
- un fort pouvoir prévisionnel sur l'état
patrimonial de chaque client (c'est-à-dire la «superstrate»
à laquelle il appartient)
- une volatilité locale (sur pas de temps mensuel) de
l'encours
- une rémanence sur le moyen-long terme d'un
déséquilibre démographique initial qui s'amortit en
plusieurs années
D'un point de vue purement théorique, ce
modèle, que nous avons appelé à «superstrates»,
est toutefois strictement identique aux cas analysés
précédemment. Notre but ici était simplement de construire
une structure pour notre banque virtuelle qui soit plus réaliste du
point de vue des valeurs de paramètres et de prouver que l'on retrouvait
toujours les faits stylisés soulevés.
16Dans le sens où les taux de transition et de
sortie adoptés paraissent plausibles si l'on interprète les
«superstrates» comme le reflet de la surface financière et les
strates comme l'état du compte
| 


