7.2 Influence de la démographie initiale
Jusqu'à présent, nous avons adopté dans
l'ensemble des simulations et analyses menées des hypothèses
démographiques très simplificatrices : nous avons en effet
considéré l'uniformité initiale de la répartition
des clients et la constance en moyenne de cette répartition dans le
temps, quel que soit l'horizon. L'enjeu était d'étudier les
influences de la mobilité des clients et de la croissance du niveau
d'inflation sur la dynamique de l'encours. Il nous fallait en
conséquence «éliminer» tout aspect démographique
dans cette dynamique.
Dans cette section, nous visons au contraire à explorer
l'influence des facteurs démographiques sur l'évolution de
l'encours. Nous pouvons notamment envisager de modifier l'uniformité de
la répartition initiale de clients, en autorisant à la date
t=0 des effectifs variables dans les différentes cellules de
clientèle. En outre, nous ne chercherons plus à assurer la
constance (en moyenne) de l'effectif Vt des clients
au cours du temps. A contrario, la base de clients évoluera constamment
et nous ferons vieillir le stock existant, en tâchant
d'interpréter les différents types de «régimes»
d'évolution de l'encours que nous mettrons ainsi en évidence.
7.2.1 Pyramide des âges et calibration des
processus d'arrivée

La pyramide des âges12 dans un pays est une
représentation graphique qui permet de visualiser la répartition
de sa population par sexe et par âge, à un moment donné.
Elle est constituée de deux histogrammes, un pour chaque sexe (avec par
convention les hommes à gauche et les femmes à droite), où
les effectifs masculins et féminins sont portés en abscisse
12Ce type de graphique est apparu en 1874 dans le
premier Atlas statistique des États-Unis. Son nom vient de sa forme
lorsque la population a une forte natalité et une forte mortalité
: il est élargi à la base et étroit au sommet. Mais cette
forme peut varier. La pyramide des âges montre en un coup d'oeil le
régime démographique et l'histoire d'un pays sur près d'un
siècle
43
(axe horizontal) et les âges en ordonnée (axe
vertical). Chaque barre associée à un sexe et à un
âge précis a une longueur proportionnelle à l'effectif de
la sous-population correspondante.
Come nous l'avons expliqué en début
d'étude, notre conviction est que la composante démographique a
potentiellement un impact significatif sur le niveau d'encours futur d'une
banque donnée. À titre d'exemple, nous constatons sur la pyramide
des âges actuelle de notre pays que l'ensemble de la
génération du baby-boom est sur le point de rentrer dans
l'âge de la retraite. Dans la mesure où ce flux
générationnel suit la période de très faible
natalité observée durant la Seconde Guerre Mondiale, le nombre de
personnes âgées est vraisemblablement sur le point d'augmenter
fortement dans un futur proche. Or les personnes âgées sont celles
qui détiennent en général le plus d'encours. En
conséquence, si une banque capte approximativement une part de
marché constante et voit la population de ses clients de plus de 60 ans
augmenter dans les mêmes proportions, on peut raisonnablement s'attendre
à ce que cette singularité démographique assure une
croissance future de l'encours probablement plus élevée que nous
n'aurions pu le supposer a priori. Cette simple remarque montre la
nécessité d'intégrer les aspects démographiques
dont nous disposons dans la calibration du modèle que nous avons
construit.
Afin de réaliser cet objectif, nous allons
opérer une projection de la pyramide des âges actuelle dans le
futur.
Pour décrire cette dernière, nous introduisons
des paramètre
(îj,t)(j,t)EÎXN
tels que îj,t E [0, 1]
est proportionnel à l'effectif de la sous-population d'âge j
dans la pyramide des âges à la date t. Nous
normalisons cette suite par rapport à la date actuelle (t=0) en
posant îá,0 =1. En ce qui concerne la
description de la pyramide actuelle, nous souhaitons en pratique épouser
sa forme globale et capter ses tendances, sans être excessivement
pointilleux. Nous prendrons donc, avec j en mois,
f
îj,0 = 1 si 216 < j < 779 (de
á = 18 ans jusqu'à 64 ans et 11 mois)
îj,0 = 0.7 - 0.3 j_780
960_780 si 780 < j < 960 (de 65 ans jusqu'à
ù = 80 ans) Autrement dit, nous avons retenu, pour
décrire la pyramide actuelle, un paramètre îj,0
constant égal à 1 jusqu'à 64 ans et 11
mois, puis nous l'avons fait décroître linéairement entre
65 ans et 80 ans de 0.7 à 0.4.
Pour projeter cette description démographique dans le
futur, nous utilisons les taux de mortalité annualisés pour 1000
personnes ÷j correspondant à l'âge j E
exprimé en mois, que nous avions déjà introduits pour
calibrer les sorties de la banque par décès. Nous poserons
(
îá,t = 1 pour t E N*
îj,t+1 = îj_1,t(1 -
10_3÷j_1) si j E - {á} pour
t E N
La projection opérée pour la pyramide des
âges est ainsi très simple. D'une part, elle est
déterministe : nous faisons l'hypothèse que les taux de
mortalité moyens sont exactement réalisés à chaque
date et qu'ils restent constants dans le temps. D'autre part, nous y supposons
implicitement une immigration nulle ainsi qu'une natalité constante
égale à celle d'aujourd'hui. En dépit de ces
hypothèses très simplificatrices, cette projection est
calquée, dans les grandes lignes, sur l'évolution probable de la
population française et a le mérite d'être facile à
calculer pour les simulations. Des raffinements sont évidemment
envisageables, mais nous souhaitons à nouveau capter ici des tendances
générales et illustrer des phénomènes typiques dont
peut rendre compte notre modèle.
44
Nous allons en premier lieu utiliser cette pyramide et ses
projections futures pour calibrer les processus d'entrée
{tt}tEN*, en faisant
l'hypothèse que é(i,j),t
suit une loi de Poisson de paramètre (et donc d'espérance)
dépendant de l'effectif dans la pyramide des âges de la
sous-population d'âge j - 1 à la date t - 1.
Plus précisément, nous supposerons donc que
V (i, j, t) EE x E - {á} x
N*, é(i,j),t ^ Poisson
(nîj-1,t-1ovol,(i,j-1))
V (i, t) E E x
N*,é(i,á),t ^ Poisson
(n)
où n est un paramètre entier
fixé et où ovol,(i,j) est le taux de
sortie volontaire de la cellule (i, j), c'est-à-dire
ovol,(i,j) =o(i,j) -
?j . Si nous reprenons les notations déjà introduites
dans
les parties précédentes,
ovol,(i,j) vaut donc 1 - ?j
ls .
En fin de compte, nous posons des processus d'arrivée
stationnaires pour les cellules correspondant à l'âge minimal
á, afin d'assurer un renouvellement continu de la base de
clientèle. En revanche, pour les autres cellules, les processus
d'entrée sont pris inhomogènes dans le temps de manière
à intégrer l'évolution de la pyramide des âges dans
la dynamique de la base de clientèle. Nous souhaitons plus
précisément paramétrer, à chaque date, des
arrivées qui soient proportionnelles aux effectifs correspondants dans
la pyramide des âges qui prévaudra à cet instant. On
suppose donc ici implicitement que la banque tend à capter une
part de marché constante! Le paramètre de la loi de
Poisson suivie par é(i,j),t est donc pris
proportionnel à deux grandeurs :
- l'effectif normalisé
îj-1,t-1 associé à l'âge
immédiatement inférieur j - 1 au sein de la pyramide
projetée de la date t - 1;
- le taux de sortie volontaire des clients de l'âge
immédiatement inférieur j - 1.
L'intérêt de cette calibration réside
dans le fait qu'elle «standardise» la distribution
démographique donnée par les projections de la pyramide que nous
avons calculées, dans le sens où elle tend à
assurer un retour vers un effectif nîj,t pour
chaque cellule (i, j) à la date
t. Par conséquent, avec cette calibration des
processus d'arrivée, la base de clientèle de la banque tend
à se calquer, en terme de distribution d'âges, sur la pyramide qui
évolue au cours du temps. n peut être
interprété comme le nombre d'arrivées mensuelles moyennes
dans chacune des cellules correspondant à l'âge
á=18 ans et 0 mois. C'est un paramètre qui
caractérise le nombre typique de personnes par cellule de
clientèle, à multiplication par le facteur d'échelle
démographique îj,t près.
Dans les simulations que nous allons à présent
effectuer, la distribution initiale de clients í0
a une importance capitale pour la dynamique future de l'encours comme
nous allons le mettre en évidence. Nous dirons dorénavant que la
banque est dans une situation initiale normale ou stable si
:
- la typologie actuelle de ses clients est l'exact reflet
démographique de la population française, dans le sens où
la distribution de sa clientèle par âge respecte les proportions
de la pyramide ;
- les s cellules correspondant à un
même âge j sont toutes constituées initialement
d'un nombre égal de clients.
La première condition impose qu'il existe p
EN* tel que í.,j,0 = Lpîj,0]
pour tout j E FL, et la seconde que Vi E E,
íi,j,0 = í',3,°
s . Autrement dit, dans un tel schéma, il
existe n E N tel que
í(i,j),0=Lnîj,0] (*) pour
toute cellule (i, j).
A contrario, nous parlerons de déséquilibre
démographique vers le bas (respectivement vers le haut) si
la population initiale de la banque n'est pas représentative de la
démographie
45
française, dans la mesure où elle
présente un excès de jeunes personnes (respectivement de
personnes âgées). La première situation est typique des
banques en ligne, qui sont apparues relativement récemment et qui ont
jusqu'à présent majoritairement séduit une
clientèle jeune. La seconde situation est plus représentative de
la clientèle actuelle de La Banque Postale, composée d'une
proportion importante de personnes d'un âge avancé.
Commençons par analyser l'évolution de
l'encours en partant d'une situation démographique normale.
Afin de discerner le facteur démographique dans ces simulations, nous y
prendrons toujours une inflation mensuelle constante it =
0.002. En outre, nous prendrons13 n=20. Voici ce
que l'on obtient comme trajectoires respectivement avec l=2 et
l=60.
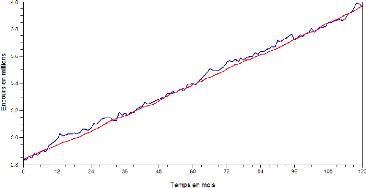
FIG. 9 - Une trajectoire pour l=2 (courbe bleue) et
l=60 (courbe rouge) de la dynamique de l'encours total avec une
inflation constante et une situation démographique normale
À première vue, on ne décèle pas
de différence dans la forme d'évolution par rapport à ce
que nous avions déjà obtenu dans les simulations
précédentes.
Toutefois, si l'on calcule le taux de croissance de l'encours
sur les dix années obtenu respectivement avec ces deux trajectoires, on
obtient 39.7% dans le cas l = 2 et 40.0% pour l
= 60, alors que le niveau d'inflation a «seulement»
augmenté de (1 + it)120 - 1 = 27.1% sur
cette même décennie. Ainsi, contrairement au cas où la
population dans la banque était constante en moyenne et
uniformément répartie entre les différentes cellules
à chaque date, pour lequel la croissance obtenue était
très voisine de celle du niveau d'inflation14, on obtient ici
une surperformance sensible par rapport à l'inflation.
La raison de ce différentiel est purement démographique : la
singularité démographique du baby-boom visible sur la
pyramide15 entraîne une augmentation continue et significative
de la sous-population des clients de plus de 65 ans au sein de
l'établissement dans les années à venir. Comme cette
population détient en moyenne plus d'encours, ce décalage
démographique interne à la banque
13Nous doublons n par rapport aux
simulations précédentes afin de ne pas faire de troncature trop
«brutale» dans la formule (*)
14Rappelons que nous avions obtenu respectivement
des croissances de 27.8% et 27.4% sur les trajectoires de la
Figure 5 page 28
15Et qui se retrouve dans la population de la
banque puisque cette dernière a une base de clientèle qui en est
le reflet en proportions
46
vient s'ajouter à l'inflation et augmente d'autant plus
l'encours global.
| 


