Modélisation et couverture des comptes courants postaux

7 Sensibilités aux paramètres et aux variables initiales

Pour pouvoir formuler des remarques qualitatives valides et faire de l'inférence statistique, nous ne pouvons nous restreindre à une seule réalisation dans chaque configuration.

L'enjeu ici est d'apprendre qualitativement et quantitativement sur les lois de certaines variables, conformément à l'ensemble du modèle que nous avons construit et des hypothèses que nous avons posées. Parmi ces variables d'«intérêt», citons par exemple les encours à horizon donné (dans la banque, dans chaque strate...) ou encore la durée de vie de l'encours dans une vision «mort de bilan» où la banque arrête de commercialiser tout produit. Pour réaliser cet objectif, il nous faut, à jeu de paramètres et d'hypothèses fixé, simuler plusieurs trajectoires (il faut en réaliser le plus grand nombre possible, la vitesse de calcul à notre disposition étant ici le facteur limitant). Nous pourrons, dès lors, calculer certaines statistiques «naturelles»⁹ relatives aux variables d'intérêt. Une telle démarche correspond à des simulations de type Monte-Carlo. La raison du recours à la simulation est notre incapacité

⁹Par exemple l'espérance empirique (c'est-à-dire la moyenne des obsevations), la variance réalisée ou encore des quantiles empiriques

37

à calculer explicitement les lois des variables aléatoires auxquelles nous nous intéressons, en raison de la trop grande complexité du modèle sous-jacent. En effet, la connaissance des différents taux de transition et de sortie, des lois des processus d'entrée ainsi que de la dynamique inflationniste ne permet pas de décrire explicitement la distribution de probabilité de vt,, où t0 est un horizon donné. Nous sommes donc ramenés à générer le plus grand nombre de scénarios pour inférer les lois des variables¹⁰. Voici le résultat d'une simulation de différentes trajectoires dans un même sous-cas (jeu de paramètres fixé). Lorsque le nombre de trajectoires augmente, on voit apparaître une forme d'«enveloppe» typique, qui est la traduction visuelle des intervalles de confiance de l'encours total à chaque date.

FIG. 7 - Un faisceau de trajectoire de l'encours total de la banque (l=2 et ir=0.002)

7.1 Influence de l'inflation et des taux de transition

Dans le cadre du modèle mathématique construit, l'inflation est l'unique déterminant de la croissance de l'encours moyen par cellule de clientèle dans la banque. Par conséquent, c'est cette grandeur qui est à l'origine de la tendance (haussière, baissière ou stable) de l'encours total dans l'établissement de crédit sur le moyen-long terme. Si l'on reprend ainsi les trajectoires simulées avec ii-=0.002 pour lE{2,60} (Figure 5 de la page 28), et que l'on calcule le

Ä120 - Ä0

taux de croissance de l'encours sur les 10 ans, on obtient respectivement 27.8%
Ä0

et 27.4%, sachant que le niveau d'inflation a augmenté de (1 + it)¹²⁰ - 1 = 27.1% sur cette même période. Les fluctuations obtenues sont dûes aux mouvements des clients au sein de la banque, et ce d'autant plus que les clients sont mobiles, c'est-à-dire que le paramètre l est faible. On observe donc dans le cas l =2 des irrégularités locales dans l'évolution de l'encours, qui peut même sur certaines périodes décroître.

En particulier, on remarquera ici que, bien que notre modèle suppose la relation déterministe Ät = (1 + ii-) _Ät-1 pour 1 < t < h entre encours moyen et inflation, l'encours total

¹⁰La loi forte des grands nombres et le théorème central limite sont implicitement «appelés» derrière cette procédure

38

dans la banque n'est pas pour autant une fonction déterministe du niveau de l'inflation sous celui-ci. La raison à cela réside dans la mobilité des clients au sein de l'établissement. Ainsi, si sur l'intervalle mensuel [t - 1, t], une proportion importante de clients passe dans des strates d'indice supérieur (correspondant à des encours plus modestes), l'encours total de la banque peut décroître sur cette même période alors que le niveau d'inflation aura été multiplié par 1 + it sur cet intervalle. Pour illustrer notre propos, nous avons simulé une trajectoire de l'encours global de la banque pour l=2 et it =0.002 sur un horizon de 17 ans (204 mois) et nous l'avons régressée sur le niveau d'inflation (normalisé à 100 en t = 0). Ce dernier est ici complètement déterministe, donné par ilt =100(1 + it)^t pour 1<t<204.

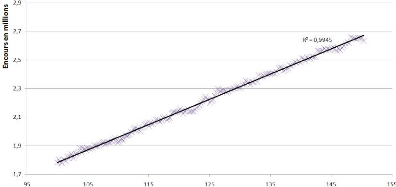
FIG. 8 - Régression du niveau de l'encours simulé sur le niveau d'inflation hors tabac

Nous disposons ainsi d'une base de comparaison avec la régression que nous avions effectuée à partir de l'encours des CCP de la Banque Postale en début d'étude. Le coefficient R² de détermination obtenu sur la trajectoire simulée est supérieur (nous avions obtenu R² =0,973 sur les données historiques). Toutefois, il est intéressant de noter que notre modèle, par la dynamique continuelle de la base de clients dans le temps, permet de rendre compte d'écarts de l'encours global par rapport au niveau d'inflation, même si l'encours moyen par cellule (donc, en fin de compte, le niveau moyen d'un dépôt de CCP) suit exactement ce niveau.

Pour saisir l'influence de la dynamique de l'inflation sur celle de l'encours, nous nous sommes intéressés, à titre d'exemple, à la distribution statistique de 60, qui n'est autre que l'encours bancaire global à un horizon d'observation de h = 60 mois. Nous reprenons pour cela, dans le cadre du modèle que nous avons construit, chacune des quatre configurations de base présentées précédemment (inflation constante ou à dynamique Ornstein-Uhlenbeck et l E{2, 60}). Nous avons généré 1000 trajectoires pour chacune de ces configurations.

Nous avons commencé par comparer les volatilités renormalisées des trajectoires d'encours sous les différents jeux de paramètres. La volatilité renormalisée Vol d'une trajectoire simulée

d'encours _{{At}tE{0,1,...,60}} est la variable aléatoire définie par

1 V ol({At}tE{0,1,...,60}) = A0

v X6 0 tt=1

(At - At-1)^2

39

Elle qualifie l'amplitude de ses variations locales (d'un mois à l'autre). Nous avons donc, dans chacun des quatre sous-cas, calculé la moyenne des 1000 volatilités empiriques associées aux trajectoires simulées. L'adoption de la valeur 60 pour le paramètre l se traduit ainsi par une diminution de 91.2% de cette volatilité par rapport au cas l = 2. L'adoption d'une dynamique inflationniste aléatoire augmente légèrement cette volatilité par rapport au cas d'une inflation constante, respectivement de 8.2% et de 8.7% pour l = 2 et l = 60. On confirme donc numériquement l'observation empirique sur les courbes tracées précédemment.

Nous faisons à présent figurer dans le tableau ci-après, pour chacun des quatre sous-cas (où nous disposons de 1000 données), la moyenne et l'écart-type empiriques, les valeurs minimale et maximale obtenues ainsi que l'intervalle empirique de confiance" à 95% de A60. Toutes les grandeurs sont exprimées en pourcentage de l'encours total initial A0 =1781050.

Statistique	At =(1 + ðt) At-1
	ðt constant ðt = ð = 0.002		dðt=a (b - rt) dt+ódWt (a, b, ó, ð0)=(0.2, 0.002, 0.0002, 0.002)
	l = 2	l = 60	l = 2	l = 60
Moyenne	112.76%	112.71%	112.65%	112.71%
Taux de croissance moyen sur la période	12.76%	12.71%	12.65%	12.71%
Ecart-type	0.90%	0.73%	2.35%	2.27%
Minimum	109.40%	110.57%	105.40%	106.46%
Maximum	115.32%	114.79%	119.28%	119.21%
[q5%, q95%]	[111.30%, 114.23%]	[111.51%, 113.89%]	[108.71%, 116.59%]	[109.11%, 116.50%]

Il convient d'abord de noter que les espérances empiriques obtenues dans les quatre sous-cas sont très proches (moins de 0.1% d'écart entre l'espérance empirique la plus élevée et la plus faible). On retrouve ici, à l'échelle d'un plus grand échantillon, que le taux de croissance moyen de l'encours sur la période est commandé par le niveau d'inflation, qui a crû de 12.73% sur la période, dans le cas de ðt =ð =0.002 que nous avons retenu.

En revanche, l'influence sur la variance des résultats apparaît très sensible à la valeur du paramètre l d'une part et au modèle retenu pour la dynamique de l'inflation d'autre part. On observe, en effet, des intervalles de confiance empiriques bien plus larges dans le cas de l'inflation aléatoire. Par ailleurs, dans le cas de l'inflation déterministe, l'écart-type obtenu est sensiblement supérieur avec la base de clientèle plus mobile. Ces remarques sont valables également dans les comparaisons des valeurs minimales et maximales.

"La notation qy avec xE[0, 1] désigne le quantile d'ordre x

40

Afin de disposer d'une base de comparaison plus «visuelle», nous faisons figurer ci-après les histogrammes des encours simulés _Ä60 à horizon h = 5 ans dans les cas l = 2 (bleu) et l=60 (rouge) avec une inflation d'abord déterministe.

On retrouve graphiquement sur les deux histogrammes les résultats numériques figurant dans le tableau : si la valeur moyenne ne varie que très peu entre les deux cas, l'écart-type lui est totalement différent. Il est ainsi près de 25% plus élevé avec la base de clientèle plus mobile. On observe ainsi une plus grande «concentration» des réalisations dans le cas l =60 où la base de clientèle est plus «rigide» et change peu de strate.

41

En comparaison, voici ce que l'on obtient avec une inflation suivant une dynamique d'Ornstein-Uhlenbeck.

L'introduction d'une inflation aléatoire se traduit par une augmentation de l'écart-type empirique d'environ 160% dans le cas l =2 et d'environ 210% dans le cas l =60. La dispersion des résultats apparaît donc bien plus importante lorsque l'inflation est aléatoire.

Ce résultat est conforme à l'intuition : en effet, le taux de croissance local de l'encours moyen, et donc de l'encours, devient stochastique lorsque l'inflation est une variable aléatoire. Notre capacité prédictive sur le moyen-long terme s'en trouve donc sensiblement affectée.

Par conséquent, une plus grande mobilité de la base de clientèle, ainsi que le caractère stochastique du niveau d'inflation, sont des facteurs qui augmentent à la fois la volatilité de l'encours et sa dispersion, c'est-à-dire sa variance, à une date considérée. Alors que les taux de transition semblent être les déterminants essentiels de la volatilité, l'influence de l'inflation prédomine largement pour l'écart-type. Ce n'est en effet que dans le cas d'une inflation connue fixée que la mobilité des clients affecte sensiblement la variance.

42