6.2 Résultats obtenus
Nous avons généré plusieurs
scénarios d'évolution de l'encours. Dans chaque simulation, et
conformément aux hypothèses mathématiques de la
modélisation adoptée, nous faisons évoluer
indépendamment la base des clients d'une part et l'encours moyen des
différentes cellules d'autre part. Nous sommes alors capables, par
produit terme à terme à chaque date,
35
de générer la trajectoire correspondante de
l'encours total dans la banque jusqu'à un certain horizon.
Inflation constante it et Ät
=(1 + it)
Ät-1 pour
1<t<h, lE{2, 60} :
Prenons à titre d'exemple h = 120 mois,
c'est-à-dire un horizon de 10 ans. Nous avons tracé ci-dessous
les trajectoires typiques d'encours obtenues dans ces conditions avec les deux
valeurs de l retenues. Nous y avons choisi it =
0.002 correspondant à une inflation annuelle de
2.4%.

FIG. 5 - Une trajectoire pour l = 2
(courbe bleue) et l = 60 (courbe rouge) de la dynamique de l'encours
total avec une inflation constante
Les valeurs 60 et 2 du paramètre l
correspondent respectivement à un changement de strate tous les
cinq ans et tous les deux mois en moyenne. On obtient dans un cas une base
clientèle stable et dans l'autre une base volatile
caractérisée par un changement de strate beaucoup plus
fréquent. La trajectoire correspondant à l=2
apparaît bien plus «erratique» en raison de la plus forte
mobilité des clients (ce qui diminue notre pouvoir prévisionnel
sur les encours futurs).
Rappelons ici que la population totale dans la banque est
globalement constante car les entrées y équilibrent les sorties.
La croissance globale de l'encours dans les deux cas est dûe à
l'inflation. Les «sursauts» correspondent quant à eux aux
mouvements aléatoires des clients au sein des strates. Leur amplitude
apparaît logiquement d'autant plus prononcée que les clients sont
mobiles.
36
Inflation à dynamique Ornstein-Uhlenbeck
{lrt} et A =(1 +
itt) Ä -1
pour 1<t<h, lE{2, 60}
:
Nous avons, toujours sur un horizon de h=120 mois,
tracé deux trajectoires simulées (l'une avec l = 2 et
l'autre avec l = 60) avec, cette fois-ci, une inflation
aléatoire. Les paramètres adoptés pour la dynamique
Ornstein-Uhlenbeck sont toujours
(a, b, a,
it0)=(0.2,0.002,0.0002,
0.002).
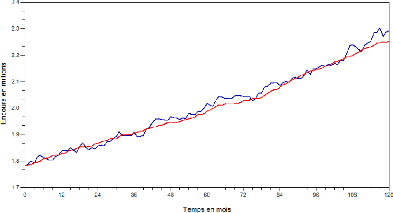
FIG. 6 - Une trajectoire pour l=2
(courbe bleue) et l=60 (courbe rouge) de la dynamique de l'encours
total avec une inflation suivant une évolution d'Ornstein-Uhlenbeck
Pour de tels paramètres, les «formes»
obtenues sont à première vue similaires. Il nous faut
générer un grand nombre de trajectoires pour tenter de
déceler les différences potentielles induites par le changement
dans l'évolution de l'inflation.
| 


