Existence et comportement asymptotique des solutions d'une équation de viscoélasticité non linéaire de type hyperbolique

Chapter 3

Global Existence and Energy Decay

Abstract

In this chapter, we prove that the solution obtained in the second chapter (Local solution ) is global in time: In addition, we show that the energy of solutions decays exponentially if m = 2 and polynomial if m > 2, provided that the initial data are small enough. The existence of the source term ( u p-2 u) forces us to use the potential well depth method in which the concept of so-called stable set appears. We will make use of arguments in [44] with the necessary modifications imposed by the nature of our problem.

3.1 Global Existence Result

In order to state and prove our results, we introduce the functional

0 t

I(t) = I(u(t)) = 1 -- I g(s)ds) 11Vu(t)11²₂ + (g 0 Vu)(t) -- b11u(t)11^p_p , (3.1)

0

and

t

J(t) = J(u(t)) = 1 2 (1-- f g(s)ds 11V u(t)11₂² + ₂(g 0 Vu)(t) -- b 11u(t)r_p , (3.2)

0

for u(t, x) E 1¹₀ (Q) , t > 0.

As in [19], the potential well depth, is defined as

d = inf uEHJ, (12)\{0}

sup A>0

J (Au) . (3.3)

The functional energy associated to (P) is defined as fallows

E(u(t),ut(t)) = E(t) = 2 1 11ut(t)11²₂ + J(t). (3.4)

Now, we introduce the stable set as follows:

W = {u E 1¹₀ (Q) : J(u) < d, I(u) > 01 U {0} . (3.5)

We will prove the invariance of the set W. That is if for some to > 0 if u(to) E W, then u(t) E W, Vt > to.

Lemma 3.1.1 d is positive constant. Proof. We have

2 t

J(Au) = A 2 ( 1 -- I g(s)ds) 11V u(t)g + (g 0 V u)(t) ^b) -- _pA^p 11u(t)r_p P. (3.6)

0

Using (G1), (G2) to get

J(Au) > K(A),

A2 2 b

where K(A) = 2 l 11Vu11₂ -- _pA^p 11u11^p_p .

By differentiating the second term in the last equality with respect to A, to get

_dAK(A) = Al lV4²

d 2 -- bA^p-1 Muk^p_p . (3.7)

1

For, Al = 0 and A2 =

(111V ug) b Muk^pp

p-2 , then we have

d _dAK(A) = O.

As K(Ai) = 0, we have K(A2) =

1 (/ 11Vu112) 2 b Muk^pp

2 p-2

1 1Vu1^22 -- p^b

111V ug) b NM^pp

p p-2

Iul^p p

=

1_b

2

p-2 (/);² (Mug)

-2 p

^p-2 (11V711122)p-2

~	1 P		-2 bp^-2 (1)		p-2 (114^pp)^-	2 p ^p-2 (IMUM2)p-2
= (1)		p P-2 b		2p -2p -2 (12 1 p-2 - p) IIVU112^-2 Mu11f3^-2 - (3.8)

By Sobolev-Poincare's inequality, we deduce that K(A2) > 0. Then, we obtain

sup {J(Au), A > 0} > sup {K(A), A > 0}

> 0. (3.9)

Then, by the definition of d, we conclude that d > 0.

Lemma 3.1.2 ([19]) W is a bounded neighbourhood of 0 in l¹₀ (a).

Proof. For u 2 W, and u 0, we have

t

(g(s)ds 11V u(t)112 + ₂ (g o V u)(t) -- pb Ilu(t)rp J(t) = 21 1 -- I

t

0

)

1 -- I g(s)ds kru(t)k2 5 + 1

2 + (g ~ ru)(t) pI(u(t))

0

(P ^p2) [ (

r / t

--> ^{(13 2-132)} [(1 -- I g(s)ds) 11V u(t)11²₂ + (g 0 V u)(t)1 .

₀ (3.10)

By using (G1) and (G2) then (3.10) becomes

t

J(t) > (p 2p2) 1 -- I g(s)ds) 11V u(t)11²₂

0

> l (p 2p2) 11Vu(t)g

then,

11V u(t)g < lp -- ( _2p 2)

J(t)

< lp -- ( 2p)

d = R. 2

Consequently, Vu 2 W we have u 2 B where

B = {u 2 A:1(Q) : 1Vu(t)1²₂ < RI . (3.11)

This completes the proof. Now, we will show that our local solution u(t, x) is global in time, for this purpose it suffices to prove that the norm of the solution is bounded, independently of t, this is equivalent to prove the following theorem.

Theorem 3.1.1 Suppose that (G1) , (G2) and (2.3) hold. if uo 2 W, u1 2 A¹₀ (Q) and

p-2

bCf, l

((^2p p -- 2) lE(0))

2

< 1, (3.12)

where C. is the best Poincare's constant. Then the local solution u(t, x) is global in time. Remark 3.1.1 Let us remark, that if there exists to 2 [0, T) such that u(to) 2 W and ut(to) 2 Aj(Q) and condition (3.12) holds for to. Then the same result of theorem 3.1.1 stays true.

Before we prove our results, we need the following Lemma, which means that, our energy is uniformly bounded and decreasing along the trajectories.

Lemma 3.1.3 ([44]) Suppose that (G1) , (G2), (2.3) hold, and let (uo, ui) 2 (Aj(Q))². Let u(t, x) be the solution of (P), then the modified energy E(t) is non-increasing function for almost every t 2 [0, T), and

d 1

dt m E(t) = --allut(t) II^- #177; 2 (g^' o Vu) (t) - ₂ g (t) 11V u(t)11²₂ - w 11out(t)112

(3.13)

< 0, Vt 2 [0, T).

Proof. By multiplying the differential equation in (P) by ut and integration over a we obtain

2

Ilut(t)g ₂ + 1 (1 -- I g(s)ds ) 11V u(t)g + ¹ ₂(g o Vu)(t) -- b Ilu(t)rp 0

d

₈

<

:

dt

t

1 1

= --allut(t)117,+ ₂ (g^' o V u) (t) -- 2 g (t) 11V u(t) I12 -- w 11V ut(t)g

1

<

2

(g^' o Vu) (t) < 0, Vt 2 [0, T) . By the definition of E(t), we conclude

d
dt

E(t) < 0. (3.14)

This completes the proof. The following lemma tells us that if the initial data ( or for some to > 0) is in the sat W, then the solution stays there forever.

Lemma 3.1.4 ([44]) Suppose that (G1) , (G2) , (2.3) and (3.12) hold. If u0 2 W, u1 2 1/₍1^- (a), then the solution u(t) 2 W, Vt > 0.

Proof. Since uo 2 W, then

I(o) = Ilvuo g -- Mud; > 0,

consequently, by continuity, there exists T,, < T such that

t

0

(I (u (t)) = 1 -- I g(s)ds 11V u(t)g + (g 0 Vu)(t) -- bllu(t)r_p > 0, Vt 2 [0, T_rri] .

This gives

t

1 1 b

J(t) = 2 (1 -- I g(s)ds ) 11V u(t)g + ₂ (g o Vu)(t) -- p Ilu(t)rp

0 (p2--p 2)

0

t

[(1 -- I g(s)ds) 11V u(t)g + (g 0 V u)(t) 1+ ^p1 gu(t))

r / t

--> (p 2-p2) [(1 -- I g(s)ds) 11V u(t)11²₂ + (g 0 Vu)(t) .

₀ (3.15)

By using (3.1) , (3.15) and the fact that

1 0

7

g(s)ds, we easily see tha

~ 2p ~

kru(t)k2 2 ~ 1 J(t)

l p ~ 2~ 2p ~

1

~ E(u(t)) (3.16)

l p ~ 2

< 2 l 1 p5, 2p2p E(0), ),t V2 [0,0T T_r]_i. .

We then exploit (G1) , (3.12) , (3.16) , and we note that thembedding l¹₀ij (a) c-- L^P (a), we have Ilu(t)11_p < CIIVu(t)11₂ (3.17)

2n

for 2 < p <

if n > 3, or p > 2 if n = 1, 2, and C = C (n, p a).).

n -- 2

Consequently, we have

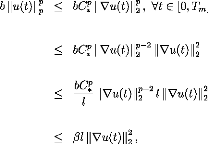
(3.18)

p-2

which means by the definition of l

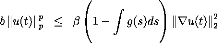
bb u(t)t)rp 0 0 1 1-- g(s)dsds) 1u(t)t)11

0

t
t

0 < 1--

1 g(s)ds A d1Vu(t)12212 Vt 2 E [0, Trri] .

where

. ·

(3.19

0

= bCbC_*^P 2p 2_l

(p (p 2)2l^E(0)0))

t

0 1

Therefore,

b Ilu(t)rp < bCf mvu(t)kp2 ,g, v 2 E [0, Tri] < bCfkru(t)kp~2 2 -IVu(t)k22)~ bCp l kru(t)kp~2 ~ 2 l kru(t)k2 2 / 0l0 IVu(t)k22)g tt 0 g(s)ds ds

_Z

0

I(t) = _@1 ~ g(s)ds _{d A}1Vu(t)k²₂)g + (g Vu)(t)t) -- b Ilu(t)r_p > 0. (3.20)

for all t 2 [0,T,] ,

By taking the fact that

p-2

lim ti-).7',7,

bCf, ( ^213 E (0)) 1 \03 -- 2) 1 j

2

< 0 < 1. (3.21)

This shows that the solution u(t) 2 W, for all t 2 [0, T_rn] . By repeating this procedure T_m extended to T.

Proof of Theorem 3.1.1.

In order to prove theorem 3.1.1, it suffices to show that the following norm

Ivu(t)I2 + 11⁷⁴(0112 , (3.22)

is bounded independently of t.

To achieve this, we use (3.4) , (3.14) and (3.15) to get

1

E(0) > E(t) = J(t) + ₂ Ilut(t)g

_{0 1 3}

p ~ 2 ~ 2 Zt

? 0

₄ @1 ~ g(s)ds A kru(t)k2 ₂ + (g ~ ru)(t) 5 2p

1 1

+₂ Mut(t)112 ² + _PI(t)

p ~ 2 ~ l kru(t)k2 ₂ + (g ~ ru)(t)~ + 1

? 2 kut(t)k2 ₂ + ¹ pI(t)

2p

(3.23)

~p ~ 2 ~ ~ ~

2 + 1

? l kru(t)k2 ₂ kut(t)k² ;

2

2p ⁾

since I(t) and (g o Vu)(t) are positive, hence

1vu(01²₂₂ + mut(t)k²₂g < CE(0),

where C is a positive constant depending only on p and 1. This completes the proof of theorem 3.1.1.

The following lemma is very useful

Lemma 3.1.5 ([44]) Suppose that (2.3) and (3.12) hold. Then

tb Ilu(t)r_p < (1 -- n) (1 -- I g (s)ds) kru(t)k² (3.24)

0

2

where n = 1 -- 0.